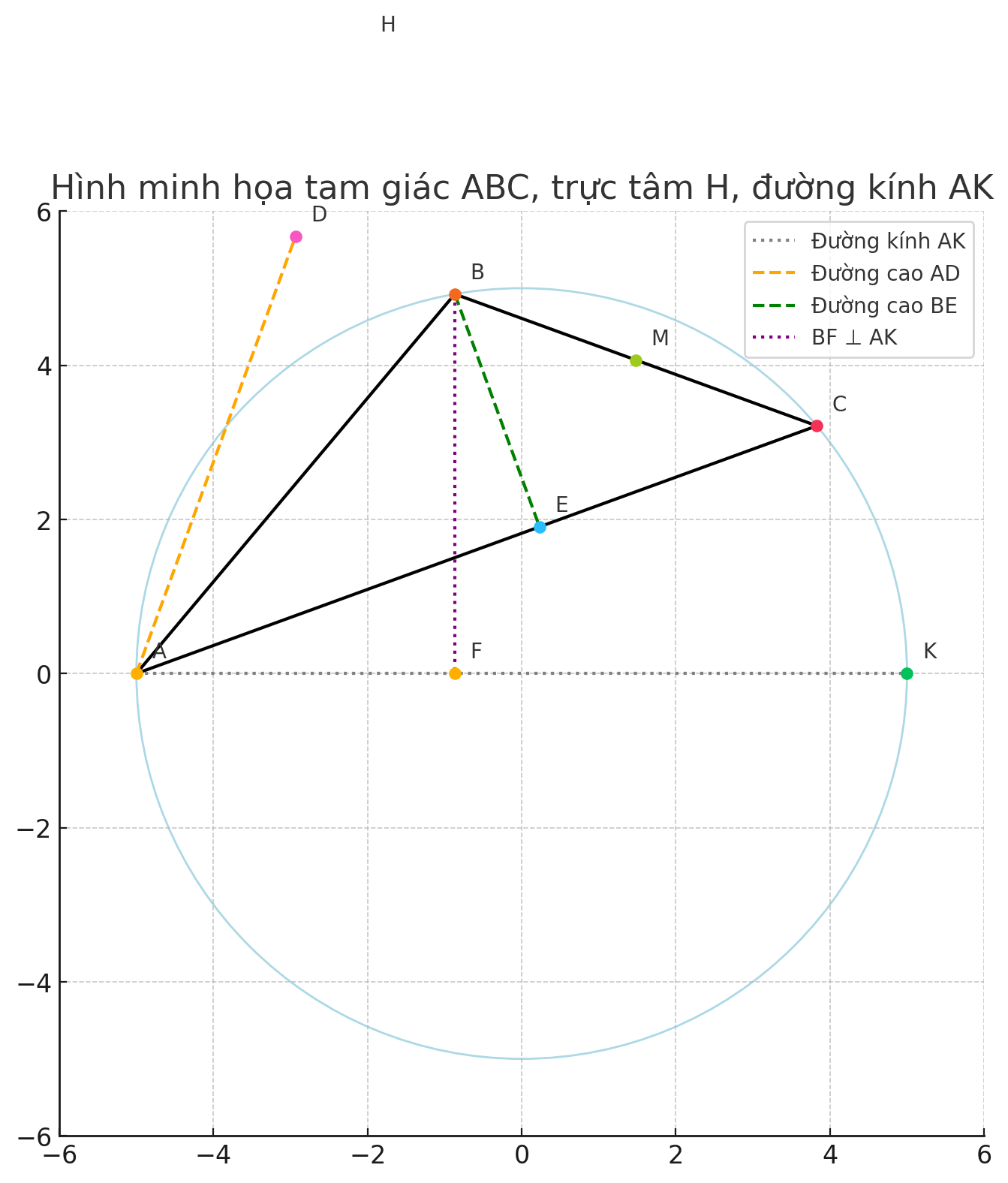
b) Gọi M là trung điểm của BC . Chứng minh M, H, K thẳng hàng.
c) Cho CH = 3cm. Tính số đo của DHE.
Quảng cáo
1 câu trả lời 199
b) Chứng minh M,H,K thẳng hàng
Sử dụng tính chất của đường trung trực, trực tâm và hình học đường tròn:
- AK là đường kính → ∠ABK=90∘, tam giác vuông tại B
- H là trực tâm tam giác ⇒ giao của các đường cao
- Trong tam giác nhọn, trực tâm H, trung điểm đáy M, và tâm đường tròn ngoại tiếp sẽ thẳng hàng trên đường Euler
→ K là điểm cuối của đường kính AK, tức điểm đối xứng của A qua tâm O → O là trung điểm AK
→ M,H,K thẳng hàng trên đường Euler của tam giác ABC
M,H,K thẳng hàng
c) Cho CH=3 cm, tính số đo góc ∠DHE
- AD⊥BC, BE⊥AC
→ Góc ∠DHE là góc giữa hai đường cao, cùng đi qua trực tâm H
→ Sử dụng tam giác vuông tại D và E để tính góc DHE
- Xét tam giác vuông AD⊥BC, BE⊥AC
- Góc ∠DHE là góc giữa hai đường cao AD và BE
- Trong tam giác ABC, góc giữa hai đường cao tại trực tâm bằng góc ∠C (góc còn lại của tam giác)
→ Vì H là giao của hai đường cao AD,BE, thì:
∠DHE=∠C
Vậy ta cần tính ∠C
Sử dụng định lý sin trong tam giác ABC nội tiếp đường tròn bán kính R=5:
sinC=CHAB(nếu biết thêm AB)
Nhưng đề bài chỉ cho CH=3 cm, chưa đủ dữ kiện để tính cụ thể số đo góc nếu không biết độ dài cạnh hoặc góc khác.
- Nếu chỉ cần suy luận, thì:
∠DHE=∠C
- Nếu biết thêm góc hoặc cạnh cụ thể của tam giác, có thể tính số đo cụ thể của ∠C, từ đó suy ra ∠DHE
Quảng cáo
Câu hỏi hot cùng chủ đề
-
240568
-
72197
-
Hỏi từ APP VIETJACK50057
-
44695












