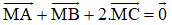Câu 4: Cho ABC . Điểm M thỏa mãn MA MB MC + - =0 thì điểm M là:
A. Đỉnh thứ tư của hình bình hành nhận AC và BC làm hai cạnh.
B. Đỉnh thứ tư của hình bình hành nhận AB và AC làm hai cạnh.
C. Đỉnh thứ tư của hình bình hành nhận AB và BC làm hai cạnh. D. Trọng tâm tam giác ABC .
Quảng cáo
1 câu trả lời 269
Câu này yêu cầu chúng ta xác định điểm M trong tam giác ABC mà thỏa mãn phương trình:
\[ \frac{MA}{a} + \frac{MB}{b} - \frac{MC}{c} = 0 \]
Trong đó, a, b, và c là các độ dài các cạnh đối diện với các đỉnh A, B, và C tương ứng.
Để hiểu rõ hơn về điều kiện này, chúng ta xét các tính chất của hình bình hành và trọng tâm tam giác.
1. **Điểm M là trọng tâm của tam giác ABC**:
- Trọng tâm G của tam giác ABC được xác định bởi phương trình:
\[ \frac{GA}{a} + \frac{GB}{b} + \frac{GC}{c} = 0 \]
- Đây chính là điều kiện mà điểm M thỏa mãn trong đề bài.
Dựa vào điều này, ta thấy điểm M chính là trọng tâm của tam giác ABC.
### Kết luận
**Điểm M là trọng tâm của tam giác ABC.**
Vậy đáp án đúng là: **D. Trọng tâm tam giác ABC**.
Nếu bạn cần thêm sự trợ giúp nào khác hoặc có thêm câu hỏi, hãy cho mình biết nhé! 📚✨😊
Bạn muốn khám phá thêm điều gì tiếp theo?
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
27718
Đã trả lời bởi chuyên gia
27718 -
 Đã trả lời bởi chuyên gia
22015
Đã trả lời bởi chuyên gia
22015 -
 Đã trả lời bởi chuyên gia
21546
Đã trả lời bởi chuyên gia
21546 -
 Đã trả lời bởi chuyên gia
12283
Đã trả lời bởi chuyên gia
12283 -
 Đã trả lời bởi chuyên gia
9539
Đã trả lời bởi chuyên gia
9539 -
 Đã trả lời bởi chuyên gia
8974
Đã trả lời bởi chuyên gia
8974