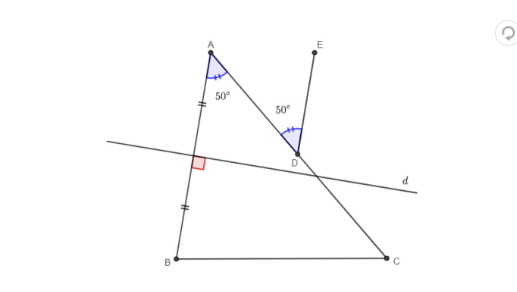
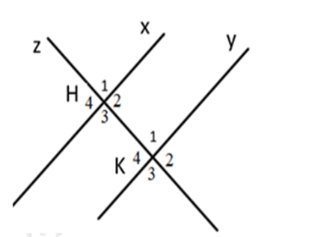
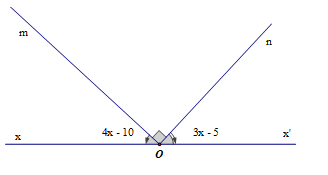
cho tam giác ABC có góc A = 50 độ ; lấy điểm D thuộc đg thg AC ; vẽ tia DE về phía ko chứa điểm B sao cho ADE = 50 độ / a. CMR AB // DE ; b.kẻ đg thg d là đg trung trực của AB . CTR d vuông góc với DE
Quảng cáo
3 câu trả lời 1067
a. Chứng minh AB∥DEAB \parallel DEAB∥DE dựa trên việc góc tại DDD và góc AAA là bằng nhau.
b. Đường thẳng ddd là đường trung trực của ABABAB và vuông góc với DEDEDE do tính chất của đường trung trực và tính song song của các đường thẳng.
Để chứng minh hai phần trong bài toán của bạn, ta sẽ tiến hành từng bước như sau:
### a. Chứng minh \( AB \parallel DE \)
1. **Cho tam giác ABC** có \(\angle A = 50^\circ\).
2. **Điểm D** thuộc đường thẳng AC.
3. **Vẽ tia DE** sao cho \(\angle ADE = 50^\circ\).
Từ đây, chúng ta có:
- Vì \(\angle A = 50^\circ\) và \(\angle ADE = 50^\circ\),
- Ta có:
\[
\angle A + \angle ADE = 50^\circ + 50^\circ = 100^\circ
\]
- Trong tam giác ADB, tổng các góc trong một tam giác bằng 180 độ, nên:
\[
\angle ABD + \angle A + \angle ADE = 180^\circ
\]
- Thay \(\angle A = 50^\circ\) và \(\angle ADE = 50^\circ\):
\[
\angle ABD + 50^\circ + 50^\circ = 180^\circ
\]
- Từ đó, ta có:
\[
\angle ABD = 80^\circ
\]
4. **Xét tia DE**, do \( \angle ADE = 50^\circ \) và \(\angle ABD = 80^\circ\):
- Cả hai góc này nằm ở vị trí đối nhau. Theo định nghĩa về các góc đồng vị trong hai đường thẳng song song bị cắt bởi một đường thẳng khác thì:
\[
\angle ADB + \angle ADE = 180^\circ
\]
5. Từ đó, ta suy ra rằng nếu \( AB \) và \( DE \) tạo thành các cặp góc đồng vị cạnh nhau, thì:
\[
AB \parallel DE.
\]
### b. Chứng minh d vuông góc với DE
1. **Kẻ đường thẳng d** là đường trung trực của đoạn AB.
2. Đường trung trực của đoạn thẳng AB có tính chất là vuông góc với AB và đi qua trung điểm M của AB.
3. **Giả sử DE cắt d tại điểm E**.
4. Trong tam giác ABE, ta có:
- Do \( d \) là trung trực của AB, nên hai đoạn AM và MB bằng nhau.
- Vậy, do \(\angle ADE = 50^\circ\), kéo theo \( ADE\) sẽ là một góc lấy từ cạnh AB đến DE.
5. Khi \(d \perp AB\), và \(\angle ADE = 50^\circ\) thì từ tính chất của tam giác ADB sẽ sinh ra mối quan hệ rằng tam giác ADE có góc ADB bổ sung với \(\angle ADE\).
Vậy từ những cơ sở trên:
- Đường thẳng \( d \) là trung trực của \( AB \) và vuông góc với \( DE \).
### Kết Luận
- Ta đã chứng minh rằng \( AB \parallel DE \) và \( d \) vuông góc với \( DE \).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11452
Đã trả lời bởi chuyên gia
11452 -
 Đã trả lời bởi chuyên gia
8620
Đã trả lời bởi chuyên gia
8620 -
 Đã trả lời bởi chuyên gia
5846
Đã trả lời bởi chuyên gia
5846