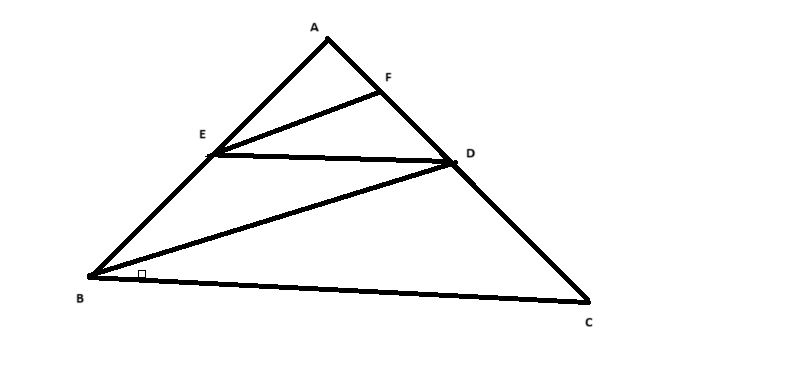
Câu a: Chứng minh tam giác \( \triangle AED \) cân

Giả thiết:
- \( \triangle ABC \) có đường phân giác \( BD \).
- Đường thẳng qua \( D \) song song với \( BC \) cắt \( AB \) tại \( E \).

Kết luận: Tam giác \( \triangle AED \) cân.

Chứng minh:

1. Vì \( BD \) là đường phân giác của \( \triangle ABC \), nên \( \frac{AD}{DC} = \frac{AB}{BC} \). (1)

2. Vì \( DE \parallel BC \) (theo giả thiết) và \( BD \) cắt \( DE \) tại \( D \), nên ta có cặp góc đồng vị \( \angle ADE \) và \( \angle DBC \) bằng nhau:
\[
\angle ADE = \angle DBC
\]

3. Đồng thời, cặp góc đồng vị \( \angle DEA \) và \( \angle BCD \) cũng bằng nhau:
\[
\angle DEA = \angle BCD
\]

4. Vì \( DE \parallel BC \), các góc tại \( A \) và \( D \) tương ứng là \( \angle EAD \) và \( \angle ABC \). Tuy nhiên, chúng ta không cần sử dụng tính chất này.

5. Xét \( \triangle BDC \) và \( \triangle EDC \):
- \( \angle BDC \) chung.
- \( DE \parallel BC \), nên \( \triangle BDC \) và \( \triangle EDC \) có tính chất đồng dạng.

Từ đó, ta có:
\[
\frac{BD}{DC} = \frac{ED}{DC} \quad (2)
\]

Nhưng từ (1) ta có:
\[
\frac{BD}{DC} = \frac{AB}{BC} = \frac{AD}{DC} = \frac{AE}{ED}
\]
Từ (1) và (2), suy ra \( AD = AE \).

Kết luận: Tam giác \( \triangle AED \) cân tại \( A \).

Câu b: Chứng minh \( EF \parallel BD \)

Giả thiết:
- \( EF \) là đường phân giác của \( \triangle AED \).
- \( BD \) là đường phân giác của \( \triangle ABC \).

Kết luận: \( EF \parallel BD \).

Chứng minh:

1. Xét \( \triangle AED \), \( EF \) là phân giác nên ta có:
\[
\frac{AE}{ED} = \frac{AF}{FD}
\]
(Do tam giác cân tại \( A \), \( F \) là trung điểm của \( ED \)).

2. Xét \( \triangle ABC \), \( BD \) là phân giác nên:
\[
\frac{AB}{BC} = \frac{AD}{DC}
\]

Kết hợp với \( AE = AD \) (do tam giác \( \triangle AED \) cân), suy ra:
\[
\frac{AE}{ED} = \frac{AD}{DC}
\]

3. Từ các tỉ lệ trên, ta thấy \( \triangle AEF \) đồng dạng với \( \triangle BDF \), và:
\[
\frac{AE}{ED} = \frac{AF}{FD} = \frac{AB}{BC} = \frac{BD}{DC}
\]

4. Do \( BD \) và \( EF \) là hai đường phân giác tương ứng trong các tam giác đồng dạng, và có tỉ lệ tương ứng bằng nhau, ta có:
\[
EF \parallel BD
\]

Kết luận: \( EF \parallel BD \) (đpcm).