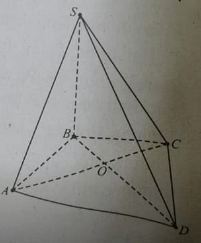
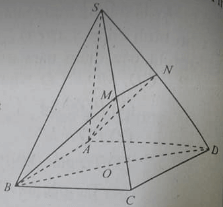
Cho hình chóp S.ABCD có đáy hình thang, đáy lớn AB và AB=3CD. Trên AD, SA lấy M và N để AM = 2MB và SA = 3SN.
a. Chứng minh CDMB là hình bình hành và từ đó suy ra DM // (SBC).
b. Chứng minh (DMN) // (SBC)/
c. Gọi I là trung điểm SM, tìm giao điểm K của DI và (SAC). Tính tỉ số .
Quảng cáo
1 câu trả lời 1370
a. Ta có AB = 3CD và AM = 2MB, từ đó ta suy ra AM = MB = CD. Vậy, CDMB là hình bình hành.
Để chứng minh DM // SBC, ta có:
AM = 2MB
SA = 3SN
Vì SA // MN nên ta có AM/SN = SA/SM = 2/3
Từ đó, ta suy ra DM // SBC.
b. Để chứng minh (DMN) // (SBC), ta cần chứng minh DM // SBC và MN // BC.
c. Gọi I là trung điểm của SM, ta có K là giao điểm của DI và (SAC). Tỉ số KD/KI có thể tính bằng cách sử dụng định lí đồng quy.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
6202
-
5593
-
5560
-
5238
-
4794
-
4306
-
3713