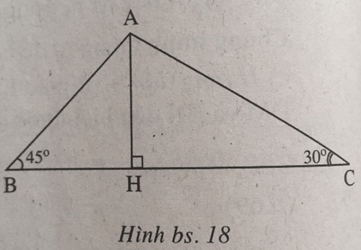Để tính độ dài các cạnh AB và AC của tam giác ABC với các góc \(\angle A = 105^\circ\), \(\angle B = 45^\circ\), và cạnh BC = 4 cm, chúng ta sẽ sử dụng định lý sin trong tam giác.

### Bước 1: Xác định các góc còn lại
Ta biết tổng các góc trong tam giác là \(180^\circ\). Vậy, góc C có thể được tính như sau:
\[
\angle C = 180^\circ - \angle A - \angle B = 180^\circ - 105^\circ - 45^\circ = 30^\circ
\]

### Bước 2: Sử dụng định lý sin
Định lý sin trong tam giác cho biết:
\[
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
\]
Ở đây, \(a\), \(b\), \(c\) là các cạnh đối diện với các góc \(\angle A\), \(\angle B\), \(\angle C\) tương ứng. Ta có cạnh \(BC = a = 4 \text{ cm}\).

- Đặt \(AB = c\)
- Đặt \(AC = b\)

### Bước 3: Tính các cạnh
Sử dụng định lý sin, ta có:
\[
\frac{BC}{\sin A} = \frac{AC}{\sin B}
\]
và
\[
\frac{BC}{\sin A} = \frac{AB}{\sin C}
\]

Ta có:
\[
\sin A = \sin 105^\circ, \sin B = \sin 45^\circ, \sin C = \sin 30^\circ
\]

Biết rằng:
\[
\sin 105^\circ = \sin (180^\circ - 75^\circ) = \sin 75^\circ = \cos 15^\circ \approx 0.9659
\]
\[
\sin 45^\circ = \frac{\sqrt{2}}{2} \approx 0.7071
\]
\[
\sin 30^\circ = 0.5
\]

Suy ra:
\[
\frac{4}{\sin 105^\circ} = \frac{b}{\sin 45^\circ}
\]

Ta tính \(b\):
\[
b = \frac{4 \sin 45^\circ}{\sin 105^\circ} = \frac{4 \cdot 0.7071}{0.9659} \approx \frac{2.8284}{0.9659} \approx 2.93 \text{ cm}
\]

Tương tự:
\[
\frac{4}{\sin 105^\circ} = \frac{c}{\sin 30^\circ}
\]

Ta tính \(c\):
\[
c = \frac{4 \sin 30^\circ}{\sin 105^\circ} = \frac{4 \cdot 0.5}{0.9659} \approx \frac{2}{0.9659} \approx 2.07 \text{ cm}
\]

### Kết quả
Do đó, độ dài các cạnh:
- \(AC \approx 2.93 \text{ cm}\)
- \(AB \approx 2.07 \text{ cm}\)