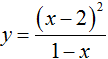cho hàm số f(x)=x3-2x2+mx-3 Tìm m để f'(x)=0 có 2 nghiệm phân biệt
Quảng cáo
2 câu trả lời 242
Để tìm \( m \) sao cho \( f'(x) = 0 \) có 2 nghiệm phân biệt, ta sẽ tính đạo hàm của hàm số \( f(x) \) và giải phương trình đạo hàm đó.
Đầu tiên, tính đạo hàm của \( f(x) \):
\[ f'(x) = 3x^2 - 4x + m \]
Sau đó, giải phương trình \( f'(x) = 0 \) để tìm các nghiệm của \( x \):
\[ 3x^2 - 4x + m = 0 \]
Để có 2 nghiệm phân biệt, discriminant của phương trình trên phải lớn hơn 0:
\[ \Delta = (-4)^2 - 4 \cdot 3 \cdot m > 0 \]
\[ 16 - 12m > 0 \]
\[ 12m < 16 \]
\[ m < \frac{4}{3} \]
Vậy, để phương trình \( f'(x) = 0 \) có 2 nghiệm phân biệt, giá trị của \( m \) phải nhỏ hơn \( \frac{4}{3} \).
## Tìm m để f'(x) = 0 có 2 nghiệm
1. Đạo hàm f(x):
`f'(x) = 3x^2 - 4x + m`
2. Điều kiện để f'(x) = 0 có 2 nghiệm phân biệt:
- `Δ > 0`
Với Δ là hệ số chênh lệch: `Δ = (-4)^2 - 4 . 3 . (m - 3) = 16 - 12m + 36 = 52 - 12m`
Để Δ > 0, ta cần giải bất phương trình: `52 - 12m > 0 ⇔ m < 4 1/3`
3. Kết luận
Để hàm số `f(x) = x^3 - 2x^2 + mx - 3 có f'(x) = 0 `có 2 nghiệm phân biệt, cần thỏa mãn điều kiện `m < 4 1/3`
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134845
Đã trả lời bởi chuyên gia
134845 -
 Đã trả lời bởi chuyên gia
26604
Đã trả lời bởi chuyên gia
26604 -
 Đã trả lời bởi chuyên gia
17064
Đã trả lời bởi chuyên gia
17064 -
 Đã trả lời bởi chuyên gia
15434
Đã trả lời bởi chuyên gia
15434 -
 Đã trả lời bởi chuyên gia
13431
Đã trả lời bởi chuyên gia
13431