cho tam giác ABC cân tại A, M là trung điểm của BC. ME vuông góc với AB, MF vuông góc với AC. Chứng minh:
AM là trung trực của BC
ME=MF và Am là trung trực của EF
EF// BC
Quảng cáo
1 câu trả lời 330
1 năm trước
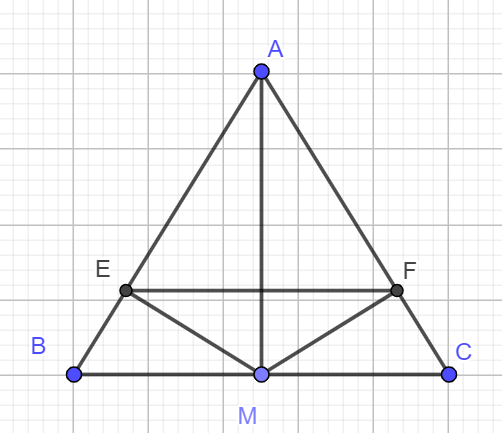
a) Xét tam giác ABC cân tại A suy ra AB=AC
M là trung điểm của BC suy ra MB=MC
Vì AM cách đều hai đầu mút của cạnh BC nên suy ra AM là đường trung trực của BC.
b) Xét tam giác MBE và tam giác MCF có:
(doME vuông góc với AB, MF vuông góc với AC)
(do ABC cân tại A)
BM=MC (giả thiết)
Suy ra tam giác MBE bằng tam giác MCF (g-c-g)
Suy ra ME=MF; BE=CF (các cặp cạnh tương ứng)
c) Ta có AB=AC, BE=CF suy raAE=AF
mà ME=MF (chứng minh trên)
vì AM cách đều hai đầu mút của cạnh EF nên suy ra AM là đường trung trực của EF.
d) Có AM là trung trực của BC suy ra
AM là trung trực của EF suy ra AM⊥EF
Suy ra EF//BC (từ vuông góc đến song song)
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
4144
Gửi báo cáo thành công!


