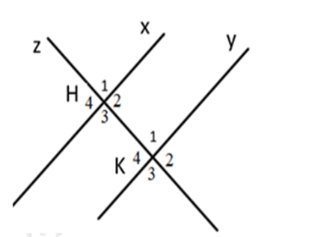
Trên hình vẽ, khi có 3 đường thẳng xx', yy và zz' cùng đi qua điểm O, ta có thể tạo ra các cặp góc đối đỉnh như sau:

Góc xOy và góc x'Oy': Đây là cặp góc đối đỉnh giữa hai đường thẳng xx' và yy'.
Góc yOz và góc y'Oz': Đây là cặp góc đối đỉnh giữa hai đường thẳng yy và zz'.
Góc zOx và góc z'Ox': Đây là cặp góc đối đỉnh giữa hai đường thẳng zz và xx'.
Vậy tổng cộng có 3 cặp góc đối đỉnh trên hình vẽ này.

Nếu có n đường thẳng phân biệt cùng đi qua 1 điểm, ta có thể tạo ra n(n-1) / 2 cặp góc đối đỉnh. Điều này xuất phát từ việc mỗi đường thẳng có thể tạo ra (n-1) cặp góc đối đỉnh với các đường thẳng khác, và ta chia đôi để loại bỏ sự trùng lặp của các cặp góc.

Vậy khi có n đường thẳng phân biệt cùng đi qua 1 điểm, ta có tổng cộng n(n-1) / 2 cặp góc đối đỉnh được tạo thành.

Trên hình vẽ, khi có 3 đường thẳng xx', yy và zz' cùng đi qua điểm O, ta có thể tạo ra các cặp góc đối đỉnh như sau:

Góc xOy và góc x'Oy': Đây là cặp góc đối đỉnh giữa hai đường thẳng xx' và yy'.
Góc yOz và góc y'Oz': Đây là cặp góc đối đỉnh giữa hai đường thẳng yy và zz'.
Góc zOx và góc z'Ox': Đây là cặp góc đối đỉnh giữa hai đường thẳng zz và xx'.
Vậy tổng cộng có 3 cặp góc đối đỉnh trên hình vẽ này.

Nếu có n đường thẳng phân biệt cùng đi qua 1 điểm, ta có thể tạo ra n(n-1) / 2 cặp góc đối đỉnh. Điều này xuất phát từ việc mỗi đường thẳng có thể tạo ra (n-1) cặp góc đối đỉnh với các đường thẳng khác, và ta chia đôi để loại bỏ sự trùng lặp của các cặp góc.

Vậy khi có n đường thẳng phân biệt cùng đi qua 1 điểm, ta có tổng cộng n(n-1) / 2 cặp góc đối đỉnh được tạo thành.