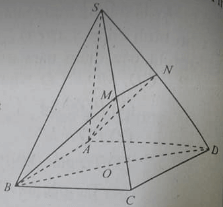
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA,SB. Điểm H thuộc đoạn SD thỏa mãn
a) Tìm giao điểm của NH và (ABCD)
b) Tìm giao điểm của đường thẳng SC và mặt phẳng (HMN)
Quảng cáo
1 câu trả lời 883
a) Xét tam giác SNH, ta có:
SH = 3/4 SD
SN = 1/2 SA = 1/2 SB = 1/4 SD
Do đó, theo định lý cosin ta có:
cos SH N = (SH^2 + SN^2 - SN^2)/(2*SH*SN) = 1/2
Hay SH N = 60 độ
Do đó, NH vuông góc với (ABCD)
Vậy giao điểm của NH và (ABCD) là H
b) Xét tam giác HMN, ta có:
MH = 1/2 MN = 1/8 SD
MN = 1/4 SD
Do đó, theo định lý cosin ta có:
cos HM N = (MH^2 + MN^2 - MN^2)/(2*MH*MN) = 1/2
Hay HM N = 60 độ
Do đó, SC vuông góc với (HMN)
Vậy giao điểm của SC và (HMN) là M
Câu trả lời:
a) H b) M
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
6206
-
5600
-
5566
-
5257
-
4804
-
4310
-
3717