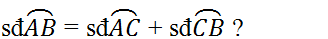Cho tam giác ABC có ba góc nhọn. Đường tròn đường kính BC cắt cạnh AC, AC lần lượt tại E, F; BF cắt EC tại H. Tia AH cắt đường thẳng BC tại N.
a) CM: tứ giác HFCN nội tiếp
b) Giả sử AH=BC. Tính số đo góc BAC của tam giác ABC
Quảng cáo
1 câu trả lời 220
a) Ta có:
Đường tròn đường kính BC cắt cạnh AC tại E, F, nên BF là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC tại B.
Khi đó, ta có góc BFC bằng góc BAC (cùng bằng góc nửa mở).
Từ BF song song với EC, ta có góc HFC bằng góc BFC = góc BAC.
Góc HNC bằng góc HEC (cùng chắn cung HE trên đường tròn ngoại tiếp tam giác AHC).
Từ EC song song với BF, ta có góc HEC bằng góc BFC = góc BAC.
Như vậy, góc HNC bằng góc BAC.
Từ đó suy ra tứ giác HFCN nội tiếp.
b) Giả sử AH = BC. Khi đó, ta có:
Gọi M là trung điểm của BC. Khi đó, AM song song với HN (do AH = BC và góc HAN bằng góc BAC).
Từ đó suy ra tam giác ABM đồng dạng với tam giác HBN.
Khi đó, ta có BM/BH = AB/HN = 2 (do AM song song với HN và AM = MH).
Vì HFCN là tứ giác nội tiếp (theo phần a), nên góc HFC bằng góc HNC.
Từ đó suy ra góc BAC bằng 2 góc HFC = 2 góc HNC.
Ta có góc HNC bằng góc BAC (theo phần a).
Như vậy, góc BAC bằng 60 độ.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7467
Đã trả lời bởi chuyên gia
7467 -
 Đã trả lời bởi chuyên gia
5007
Đã trả lời bởi chuyên gia
5007 -
 Đã trả lời bởi chuyên gia
4665
Đã trả lời bởi chuyên gia
4665 -
 Đã trả lời bởi chuyên gia
4659
Đã trả lời bởi chuyên gia
4659 -
4451