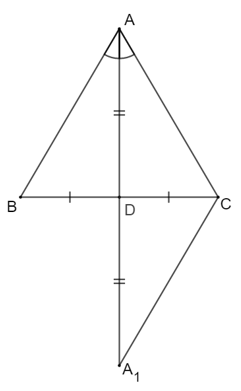
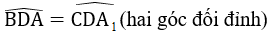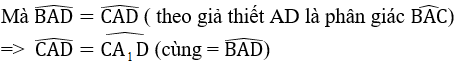Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Gợi ý: Trong ΔABC, nếu AD là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn DA1, sao cho DA1 = AD.
Quảng cáo
1 câu trả lời 469
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 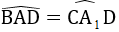
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5832
Đã trả lời bởi chuyên gia
5832 -
 Đã trả lời bởi chuyên gia
4150
Đã trả lời bởi chuyên gia
4150