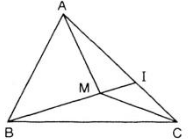
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC.
So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA.
Quảng cáo
1 câu trả lời 455
Theo giả thiết, điểm M nằm trong tam giác ABC nên điểm M không nằm trên cạnh AC.
⇒ A, M, I không thẳng hàng.
Xét bất đẳng thức tam giác trong ΔAMI:
MA < MI + IA
⇒ MA + MB < MB + MI + IA (cộng cả hai vế với MB)
hay MA + MB < IB + IA (vì MB + MI = IB).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5832
Đã trả lời bởi chuyên gia
5832 -
 Đã trả lời bởi chuyên gia
4150
Đã trả lời bởi chuyên gia
4150
Gửi báo cáo thành công!