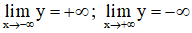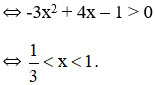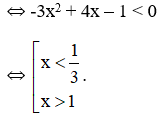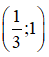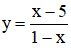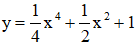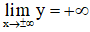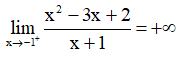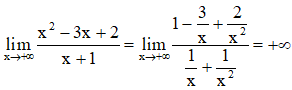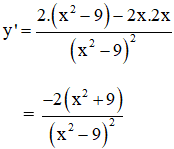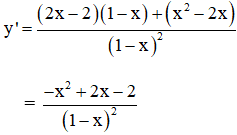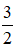+ Giới hạn:

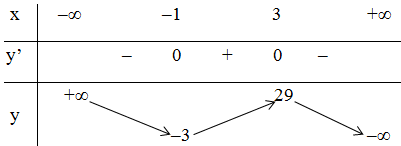
+ Bảng biến thiên:

Kết luận:

Hàm số đồng biến trên (-1; 3)

Hàm số nghịch biến trên (-∞; -1) và (3; +∞).

Hàm số đạt cực đại tại x = 3, yCĐ = 29.

Hàm số đạt cực tiểu tại x = -1; $y_{CT}=-3$

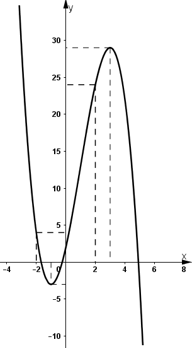
- Đồ thị:

+ Giao với trục tung tại (0; 2).

+ Đi qua các điểm (-2; 4); (2; 24).

a)Cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:

Quy tắc 1:

1. Tìm tập xác định.

2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2:

1. Tìm tập xác định.

2. Tính f'(x). Giải phương trình f'(x) = 0 và kí hiệu xi (i = 1, 2, 3, ...) là các nghiệm của nó.

3. Tính f"(x) và f"(xi)

4. Nếu f"(xi) > 0 thì xi là điểm cực tiểu.

Nếu f"(xi) < 0 thì xi là điểm cực đại.

Dựa vào Quy tắc 2, ta có:

y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại.

y"(-1) = y"(1) = 8 > 0 ⇒ x = ±1 là hai điểm cực tiểu.

- Điều kiện đồng biến, nghịch biến của hàm số:

Cho hàm số y = f(x) có đạo hàm trên khoảng K.

+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.

+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.

- Xét hàm số

+ Hàm số đồng biến

+ Hàm số nghịch biến

Vậy hàm số đồng biến trên 

nghịch biến trên các khoảng 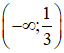 và (1; +∞)

- Xét hàm số 

Ta có: D = R \ {1}

 ∀ x ∈ D.

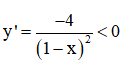
⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).

Đồ thị cắt trục tung tại điểm P(0;-1), khi đó phương trình tiếp tuyến tại điểm P(0; -1) là:

y = y'(0).(x - 0) - 1

hay y = -2x - 1

Vậy phương trình tiếp tuyến cần tìm là: y = -2x – 1.

Với m = 1, hàm số trở thành 

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

+ Giới hạn:

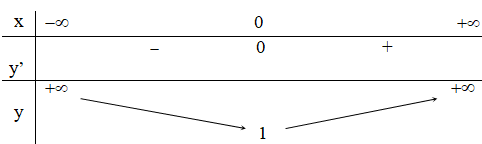
+ Bảng biến thiên:

Kết luận:

Hàm số đồng biến trên (0; +∞)

Hàm số nghịch biến trên (-∞; 0)

Hàm số có điểm cực tiểu là (0; 1).

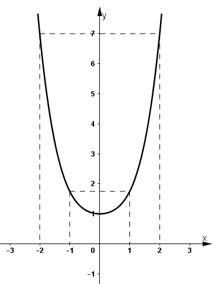
- Đồ thị:

+ Đồ thị nhận trục Oy là trục đối xứng.

+ Đồ thị cắt trục tung tại (0; 1).

+ Đồ thị hàm số đi qua (-1; 1,75); (1; 1,75); (-2; 7); (2; 7).

+ 

⇒ đồ thị có tiệm cận đứng là x = -1.

+ Lại có

⇒ đồ thị không có tiệm cận ngang.

Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.

Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)

⇒ độ dài cạnh còn lại là : 8 – x (cm)

⇒ Diện tích của hình chữ nhật là:

Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng $16c{m}^2$.

TXĐ: D = R

y"(-1) = -20 + 6 = -14 < 0

⇒ x = -1 là điểm cực đại của hàm số.

y"(1) = 20 – 6 = 14 > 0

⇒ x = 1 là điểm cực tiểu của hàm số.

Tập xác định: D = R \ {±3}

y’ < 0 với ∀ x ∈ D.

y' không xác định tại x = ±3

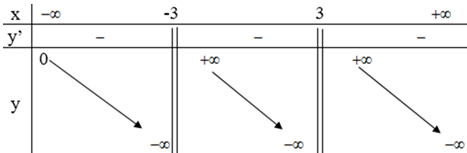
Bảng biến thiên:

Vậy hàm số nghịch biến trong các khoảng (-∞ ; -3); ( -3; 3) và (3; +∞ ).

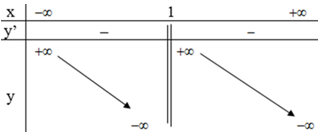
Tập xác định: D = R \ {1}

y’ < 0 với ∀ x ∈ D (vì –x2 + 2x – 2 < 0).

y' không xác định tại x = 1

Bảng biến thiên:

Vậy hàm số nghịch biến trong các khoảng (-∞ ;1) và (1 ; +∞)

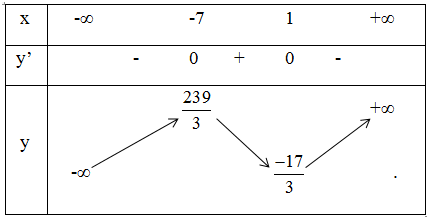
Tập xác định : D = R

y' = x2 + 6x - 7

y' = 0 ⇔ x = -7 hoặc x = 1

Ta có bảng biến thiên:

Vậy hàm số đồng biến trong các khoảng (-∞ ; -7) và (1 ; +∞); nghịch biến trong khoảng (-7; 1).

Tập xác định : D = R

y' = 3 – 2x

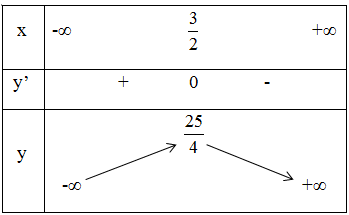
y’ = 0 ⇔ 3 – 2x = 0 ⇔ x = 

Ta có bảng biến thiên:

Vậy hàm số đồng biến trong khoảng (-∞; 3/2) và nghịch biến trong khoảng (3/2 ; + ∞).

Xét hàm số y = x3 có đạo hàm y’ = 3x2 ≥ 0 với mọi số thực x và hàm số đồng biến trên toàn bộ R. Vậy khẳng định ngược lại với định lý trên chưa chắc đúng hay nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó không nhất thiết phải dương (âm) trên đó.