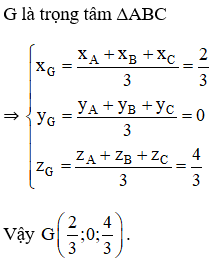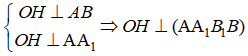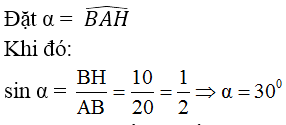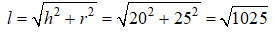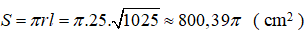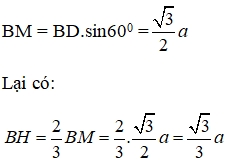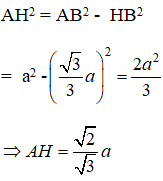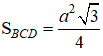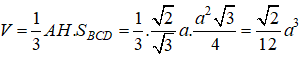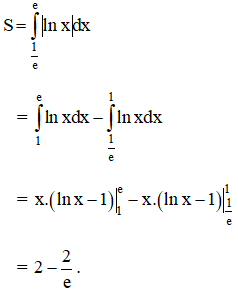⇒ Một vecto pháp tuyến của mặt phẳng (MNP) là $\overrightarrow{n}$(1;-4;5)

Phương trình tổng quát của mặt phẳng (MNP) với M(1; 1; 1), N(4; 3; 2), P(5; 2; 1)là : (x-1)-4(y-1)+5(z-1)=0

Hay x - 4y + 5z - 2 = 0

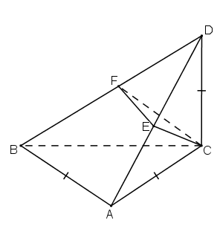
* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA

Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.

Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:

AM = AI ( tính chất hai tiếp tuyến cắt nhau)

* Tương tự có BM = BI.

* Xét hai tam giác AMB và tam giác AIB có:

AM = AI

BM = BI

AB chung

Suy ra: ∆ AMB = ∆ AIB ( c.c.c)

Tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước là đường trung trực của đoạn thẳng AB

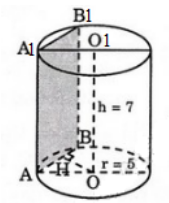
Mặt phẳng (P) song song với trục và cách trục 3cm, cắt hình trụ theo thiết diện là tứ giác $A{A}_1{B}_{1}B$.

Gọi H là trung điểm của AB.

Ta có 

SAA1B1B = AB. AA1 = 8. 7 = 56 (cm2)

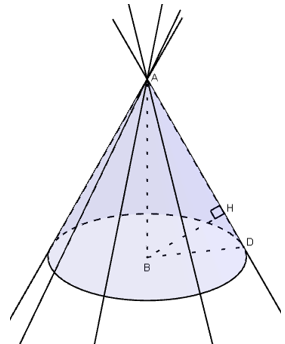
Từ B vẽ đường thẳng vuông góc với d và cắt d tại H.

Ta có BH = 10cm = d(B,d)

Vậy đường thẳng d nằm trên mặt nón có đỉnh là A, trục là đường thẳng AB và góc ở đỉnh là 2α = $60°$

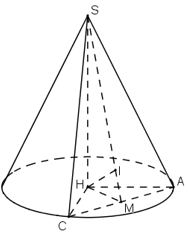
a. Độ dài đường sinh của hình nón đã cho là:

Diện tích xung quanh của hình nón đã cho là;

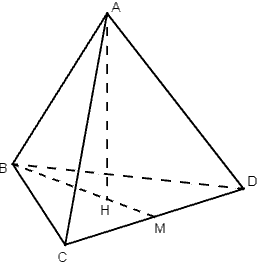
Gọi ABCD là tứ diện đều cạnh a.

Gọi H là tâm đường tròn ngoại tiếp tam giác BCD

⇒ HB = HC = HD nên H nằm trên trục đường tròn ngoại tiếp tam giác BCD. (1)

Lại có: AB = AC = AD vì ABCD là tứ diện đều

⇒ HA là trục đường tròn ngoại tiếp tam giác BCD

⇒ HA ⊥ (BCD)

Vì tam giác BCD là tam giác đều nên H đồng thời trọng tâm tam giác BCD. Gọi M là trung điểm của CD.

Xét tam giác BCD ta có:

Áp dụng định lí pytago vào tam giác vuông AHB ta được:

Diện tích tam giác đều BCD cạnh a là: 

Do đó, thể tích khối tứ diện đều ABCD là: 

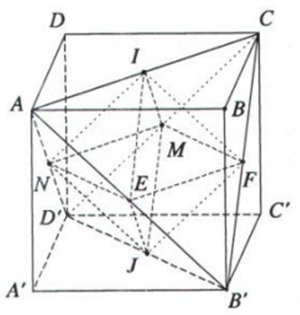
ABCD.A’B’C’D’ là hình lập phương cạnh a nên các mặt là các hình vuông cạnh a

Tứ diện AB’CD’ có các cạnh là các đường chéo của các mặt bên hình lập phương ABCD.A’B’C’D’ nên tứ diện AB’CD’ có các cạnh bằng nhau ⇒ AB’CD’ là tứ diện đều

Cạnh của tứ diện đều AB’CD’ bằng độ dài đường chéo của hình vuông cạnh a và bằng a√2

Khối bát diện đều có 6 đỉnh và 12 cạnh

* Gọi a là số cạnh, b là số mặt của khối đa diện.

Nếu khối đa diện có các mặt là tam giác thì mỗi mặt có ba cạnh. Trong ba cạnh đó mỗi cạnh lần lượt là cạnh chung của hai mặt.

Ta có 3b = 2a. Nghĩa là b chẵn.

Mà 2a chia hết cho 2 nên 3b cũng chia hết cho 2

⇒ b chia hết cho 2 hay b là số chẵn.

* Ví dụ: hình tứ diện đều có 4 mặt

- Các mặt của hình lăng trụ ABCDE.A’B’C’D’E’là: ABB’A’, BCC’B’, CDD’C’, DEE’D’, EAA’E’, ABCDE, A’B’C’D’E’

- Các mặt của hình chóp S.ABCDE là: SAB, SBC, SCD, SDE, SAE, ABCDE

Diện tích cần tính là:

Theo ý nghĩa cơ học của đạo hàm ta có: