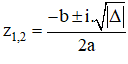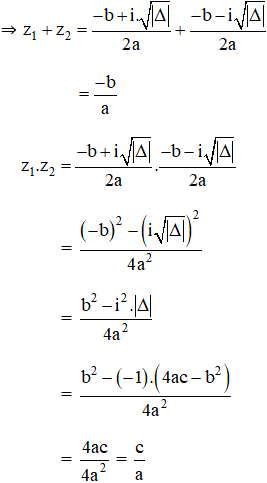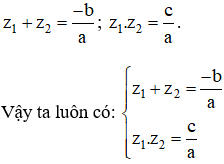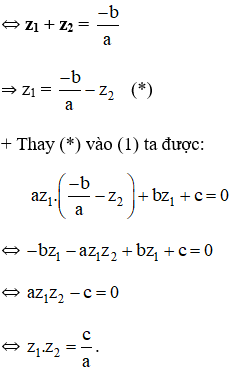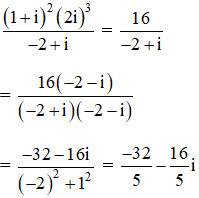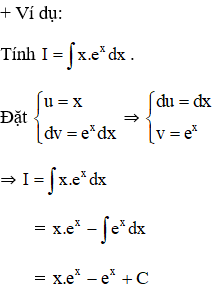Ngọc Anh
Sắt đoàn
0
0
Câu trả lời của bạn: 15:49 21/07/2020
Cho số phức z = a + bi (a, b ∈ R) thì số phức liên hợp của số phức z kí hiệu là z = a - bi
Số phức z bằng số phức liên hợp z− của nó khi và chỉ khi z là số thự
Câu hỏi:
Câu trả lời của bạn: 15:49 21/07/2020
Câu hỏi:
Câu trả lời của bạn: 15:49 21/07/2020
Cách 1 :
Phương trình az2 + bz + c = 0 có Δ = b2 - 4ac
+ TH1 : Δ < 0, phương trình có hai nghiệm phức
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
Cách 2 :
Câu trả lời của bạn: 15:49 21/07/2020
α + β = (1 - 2i) + 6i = 1 + 4i;
α – β = (1 - 2i) - 6i = 1 - 8i
Câu trả lời của bạn: 15:49 21/07/2020
Phần thực: 0, phần ảo: -7
Câu trả lời của bạn: 15:49 21/07/2020
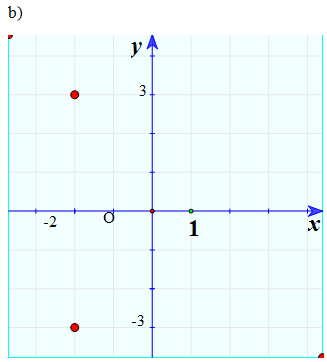
Hai điểm đối xứng nhau qua Oy.
Câu trả lời của bạn: 15:49 21/07/2020
| Số phức Phần thực Phần ảo | ||
| -3 + 5i | -3 | 5 |
| 4 - i√2 | 4 | -√2 |
| 0 + πi | 0 | π |
| 1 + 0i | 1 | 0 |
Câu trả lời của bạn: 15:49 21/07/2020
Câu trả lời của bạn: 15:49 21/07/2020
+ Phương pháp nguyên hàm từng phần:
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x).v’(x)dx = u(x).v(x) - ∫v(x).u’(x)dx
Hay viết gọn: ∫udv = uv - ∫vdv.
Câu trả lời của bạn: 15:49 21/07/2020