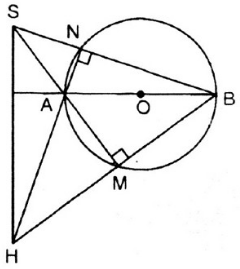
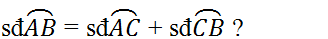Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
Quảng cáo
1 câu trả lời 568
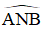
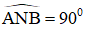
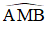
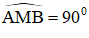
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Kiến thức áp dụng
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7467
Đã trả lời bởi chuyên gia
7467 -
 Đã trả lời bởi chuyên gia
5007
Đã trả lời bởi chuyên gia
5007 -
 Đã trả lời bởi chuyên gia
4665
Đã trả lời bởi chuyên gia
4665 -
 Đã trả lời bởi chuyên gia
4659
Đã trả lời bởi chuyên gia
4659 -
4451
Gửi báo cáo thành công!