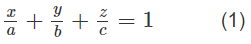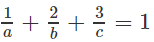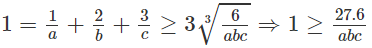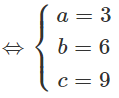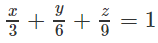Lập phương trình của mặt phẳng (α) đi qua điểm M(1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất.
Quảng cáo
1 câu trả lời 4501
Gọi giao điểm của (α) với ba tia Ox, Oy, Oz lần lượt là A(a; 0; 0), B(0; b; 0), C(0; 0 ; c) (a, b, c > 0).
Mặt phẳng (α) có phương trình theo đoạn chắn là:
Do (α) đi qua M(1; 2; 3) nên ta thay tọa độ của điểm M vào (1):
Thể tích của tứ diện OABC là:
Áp dụng bất đẳng thức Cô-si ta có:
⇒ abc 27.6 ⇒ V 27
Ta có: V đạt giá trị nhỏ nhất ⇔ V = 27
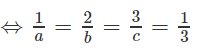
Vậy phương trình mặt phẳng () thỏa mãn đề bài là:
hay 6x + 3y + 2z – 18 = 0
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393 -
 Đã trả lời bởi chuyên gia
67790
Đã trả lời bởi chuyên gia
67790 -
 Đã trả lời bởi chuyên gia
31001
Đã trả lời bởi chuyên gia
31001 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
Trong không gian Oxyz, mặt cầu tâm I(-1;2;-3) và đi qua điểm A(2;0;0) có phương trình là:
A.
B.
C.
D.
28197 -
 Đã trả lời bởi chuyên gia
16270
Đã trả lời bởi chuyên gia
16270