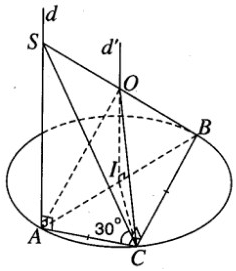
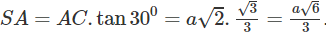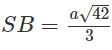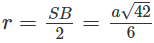Cho tam giác vuông cân ABC có cạnh huyền AB = 2a. Trên đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC), lấy một điểm S khác A, ta được tứ diện SABC. Tính bán kính của mặt cầu ngoại tiếp tứ diện SABC trong trường hợp mặt phẳng (SBC) tạo với mặt phẳng (ABC) một góc bằng 300.
Quảng cáo
1 câu trả lời 837
Trường hợp mặt phẳng (SBC) tạo với mặt phẳng (ABC) một góc 30 thì góc của hai mặt phẳng đó chính là góc SCA. Thực vậy vì SA (ABC) mà ACCB nên ta có SC ⊥ CB. Do đó ∠SCA = 30.
Vì AB = 2a nên ta có AC = a ta suy ra
Gọi r là bán kính mặt cầu ngoại tiếp tứ diện khi SCA = 30
Ta có r = SB/2 = OA = OB = OC = OS, trong đó
Vậy
Do đó
Ta suy ra
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
66238
Đã trả lời bởi chuyên gia
66238 -
 Đã trả lời bởi chuyên gia
26134
Đã trả lời bởi chuyên gia
26134 -
 Đã trả lời bởi chuyên gia
19056
Đã trả lời bởi chuyên gia
19056 -
 Đã trả lời bởi chuyên gia
13634
Đã trả lời bởi chuyên gia
13634