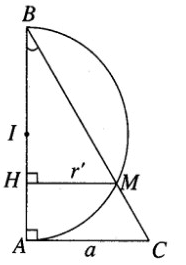
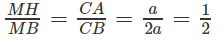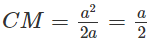Trong mặt phẳng () , cho tam giác ABC vuông tại A có cạnh AC = a và có cạnh huyền BC = 2a. Cũng trong mặt phẳng () đó cho nửa đường tròn đường kính AB cắt cạnh BC tại M. Chứng minh rằng giao tuyến của hai mặt tròn xoay đó là một đường tròn. Hãy xác định bán kính của đường tròn đó.
Quảng cáo
1 câu trả lời 517
Khi quay xung quanh trục AB, giao điểm M của nửa đường tròn đường kính AB và cạnh CD sẽ tọ nên giao tuyến của mặt nón và mặt cầu.
Vẽ MH ⊥ AB
Ta có:
Mặt khác ta có = CM.CB nên ta có
Do đó: BM = CB − CM = 3a/2 và HM = 3a/4
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
66238
Đã trả lời bởi chuyên gia
66238 -
 Đã trả lời bởi chuyên gia
26134
Đã trả lời bởi chuyên gia
26134 -
 Đã trả lời bởi chuyên gia
19056
Đã trả lời bởi chuyên gia
19056 -
 Đã trả lời bởi chuyên gia
13634
Đã trả lời bởi chuyên gia
13634
Gửi báo cáo thành công!