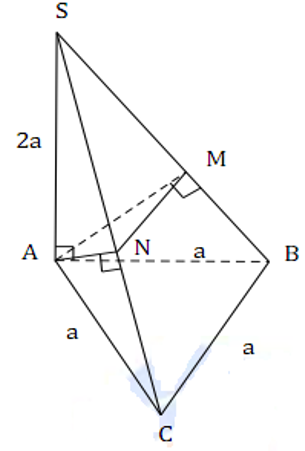
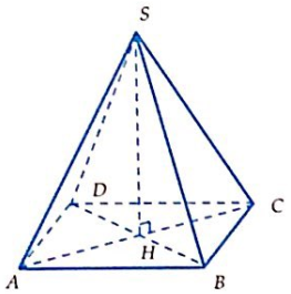
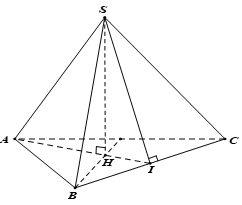
Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt phẳng của nó là một số không đổi.
Quảng cáo
1 câu trả lời 609
Ta có tứ diện đều ABCD, M là một điểm trong của nó. Gọi V là thể tích, S là diện tích mỗi mặt của tứ diện đều ABCD, lần lượt là khoảng cách từ M đến các mặt (BCD), (CDA), (DAB), (ABC).
Khi đó ta có:
V =
= S()/3
Từ đó suy ra = 3V/S
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11164
Đã trả lời bởi chuyên gia
11164 -
 Đã trả lời bởi chuyên gia
10231
Đã trả lời bởi chuyên gia
10231
Gửi báo cáo thành công!