Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;5). Số mặt phẳng đi qua M và cắt các trục Ox, Oy, Oz tại A, B, C sao cho OA = OB = OC (A, B, C không trùng với gốc tọa độ O) là:
A. 8
B. 3
C. 4
D. 1
Quảng cáo
1 câu trả lời 3180
Đáp án C
Phương pháp
+) Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c 0) viết phương trình mặt phẳng (P) đi qua A, B, C dạng đoạn chắn.M(P)=> Thay tọa độ điểm M vào phương trình mặt phẳng (P).
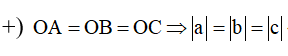
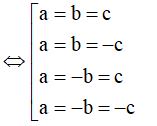
+) Ứng với mỗi trường hợp tìm các ẩn a, b, c tương ứng
Cách giải
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c 0) khi đó phương trình mặt phẳng đi qua A, B, C là
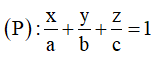
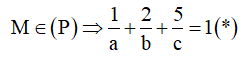
![]()
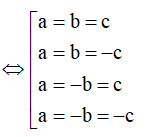
TH1: a=b=c thay vào (*) có
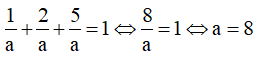
![]()
TH2: a=b=-c thay vào (*) có
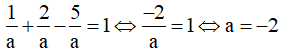
![]()
TH3: a=-b=c thay vào (*) có
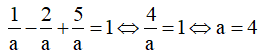
![]()
TH4: a=-b=-c thay vào (*) có
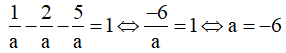
![]()
Vậy có 4 mặt phẳng thỏa mãn.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340 -
 Đã trả lời bởi chuyên gia
67779
Đã trả lời bởi chuyên gia
67779 -
 Đã trả lời bởi chuyên gia
30976
Đã trả lời bởi chuyên gia
30976 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
Trong không gian Oxyz, mặt cầu tâm I(-1;2;-3) và đi qua điểm A(2;0;0) có phương trình là:
A.
B.
C.
D.
28189 -
 Đã trả lời bởi chuyên gia
16267
Đã trả lời bởi chuyên gia
16267


