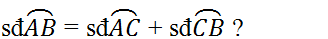Cho đường tròn tâmO đường kính AB .kẻ tiếp tuyến tại B với dường tròn O trên tiếp tuyến lấy P sao cho BP >OB . qua A kẻ đường thẳng song song với OP cắt ( O) tại Q chứng minh PQ là tiếp tuyến của (O)
Quảng cáo
1 câu trả lời 42
1 ngày trước
Để chứng minh PQ là tiếp tuyến của đường tròn (O), chúng ta cần chứng minh PQ vuông góc với bán kính OQ tại điểm Q.
Dưới đây là các bước chứng minh chi tiết:
Xác định các góc bằng nhau từ giả thiết song song:
Gọi I là giao điểm của OP và BQ. Vì AQ song song với OP (giả thiết), ta có:
Góc OAQ bằng góc POB (hai góc ở vị trí đồng vị).
Góc AQC bằng góc QOP (hai góc ở vị trí so le trong).
Chứng minh tam giác OAQ cân:
Xét tam giác OAQ có OA = OQ (cùng là bán kính của đường tròn O). Do đó, tam giác OAQ cân tại O, suy ra góc OAQ bằng góc OQA.
Chứng minh hai tam giác bằng nhau:
Từ các điều trên, ta suy ra góc POB bằng góc POQ (vì cùng bằng các góc bằng nhau của tam giác cân OAQ).
Xét tam giác OBP và tam giác OQP có:
Cạnh OB = OQ (cùng là bán kính đường tròn O).
Góc POB = góc POQ (chứng minh trên).
Cạnh OP chung.
Vậy tam giác OBP bằng tam giác OQP theo trường hợp cạnh - góc - cạnh.
Kết luận:
Vì tam giác OBP bằng tam giác OQP nên các góc tương ứng của chúng bằng nhau. Suy ra góc OQP bằng góc OBP.
Mà PB là tiếp tuyến của đường tròn (O) tại B nên góc OBP bằng 90 độ.
Do đó, góc OQP cũng bằng 90 độ.
Điều này chứng tỏ PQ vuông góc với bán kính OQ tại Q. Vậy PQ là tiếp tuyến của đường tròn (O).
Dưới đây là các bước chứng minh chi tiết:
Xác định các góc bằng nhau từ giả thiết song song:
Gọi I là giao điểm của OP và BQ. Vì AQ song song với OP (giả thiết), ta có:
Góc OAQ bằng góc POB (hai góc ở vị trí đồng vị).
Góc AQC bằng góc QOP (hai góc ở vị trí so le trong).
Chứng minh tam giác OAQ cân:
Xét tam giác OAQ có OA = OQ (cùng là bán kính của đường tròn O). Do đó, tam giác OAQ cân tại O, suy ra góc OAQ bằng góc OQA.
Chứng minh hai tam giác bằng nhau:
Từ các điều trên, ta suy ra góc POB bằng góc POQ (vì cùng bằng các góc bằng nhau của tam giác cân OAQ).
Xét tam giác OBP và tam giác OQP có:
Cạnh OB = OQ (cùng là bán kính đường tròn O).
Góc POB = góc POQ (chứng minh trên).
Cạnh OP chung.
Vậy tam giác OBP bằng tam giác OQP theo trường hợp cạnh - góc - cạnh.
Kết luận:
Vì tam giác OBP bằng tam giác OQP nên các góc tương ứng của chúng bằng nhau. Suy ra góc OQP bằng góc OBP.
Mà PB là tiếp tuyến của đường tròn (O) tại B nên góc OBP bằng 90 độ.
Do đó, góc OQP cũng bằng 90 độ.
Điều này chứng tỏ PQ vuông góc với bán kính OQ tại Q. Vậy PQ là tiếp tuyến của đường tròn (O).
Be Thong
· 1 ngày trước
Vẽ hình sao vậy bn chỉ tui với
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7447
Đã trả lời bởi chuyên gia
7447 -
 Đã trả lời bởi chuyên gia
5002
Đã trả lời bởi chuyên gia
5002 -
 Đã trả lời bởi chuyên gia
4658
Đã trả lời bởi chuyên gia
4658 -
 Đã trả lời bởi chuyên gia
4657
Đã trả lời bởi chuyên gia
4657 -
4446
Gửi báo cáo thành công!