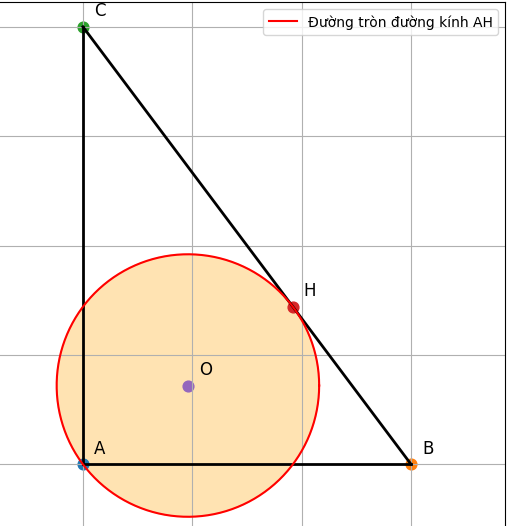
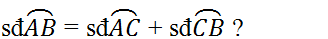Cho tam giác ABC vuông tại A có AB = 3, AC = 4, kẻ đường cao AH, đường tròn (o) đường kính AH cắt AB và AC tại M và N. Tính diện tích phần tam giác nằm ngoài hình tròn (o)
Quảng cáo
2 câu trả lời 161
1. Tính các đoạn cần thiết
- Tam giác vuông tại A, ta có: BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25
⇒ BC = 5
- Trong tam giác vuông tại A: AH = = = 2,4
Vậy bán kính đường tròn (O) là: R = = 1,2
- Diện tích tam giác ABC:
SABC = .AB.AC = .3.4 = 6
- Diện tích phần tam giác nằm ngoài đường tròn
+ Đường tròn (O) đường kính AH là đường tròn trong góc vuông A, cắt hai cạnh AB và AC tại M và N.
+ Diện tích phần tam giác nằm ngoài hình tròn:
Sngòai = SABC − S bán phần nằm trong đường tròn
+ Bán phần trong đường tròn là tam giác nhỏ AMN.
Vì M và N nằm trên AB và AC, và đường tròn đường kính AH ⇒ tam giác AMN là tam giác vuông tại A, có cạnh AH là đường cao: SAMN = .AM.AN = .R.R = .(1,2)2 = 0,72
Do đó: Sngòai = 6 − 0,72 = 5,28
Vậy: Sngòai đường tròn = 5,28
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7447
Đã trả lời bởi chuyên gia
7447 -
 Đã trả lời bởi chuyên gia
5002
Đã trả lời bởi chuyên gia
5002 -
 Đã trả lời bởi chuyên gia
4658
Đã trả lời bởi chuyên gia
4658 -
 Đã trả lời bởi chuyên gia
4657
Đã trả lời bởi chuyên gia
4657 -
4446