8. Cho hình chóp tứ giác đều S ABCD, có cạnh đáy bằng và cạnh bên bằng
. Tính thể tích hình chóp
Quảng cáo
8 câu trả lời 252
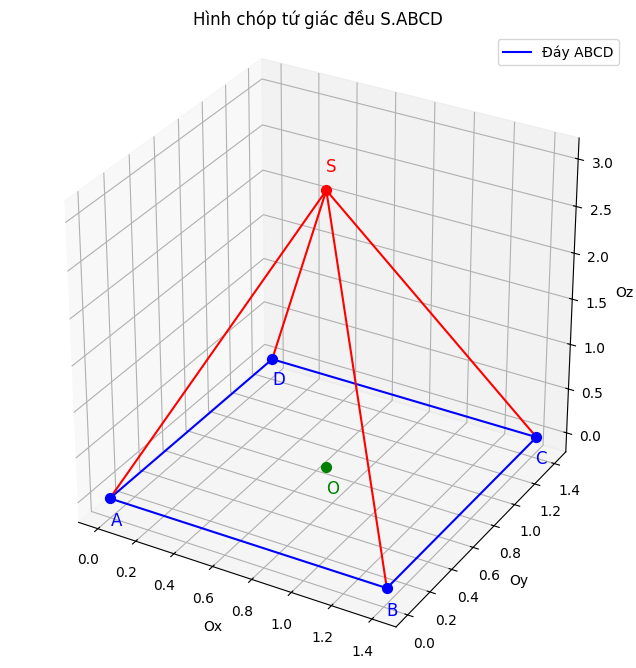
+ Đáy ABCD là hình vuông cạnh , nên diện tích đáy là: Sđáy = = 2a2
+ Gọi O là trung điểm của ABCD (tâm hình vuông)
Vì S.ABCD là hình chóp tứ giác đều, S nằm thẳng trên O,
và SO ⊥ (ABCD) => SO = h chính là chiều cao cần tìm.
Khoảng cách từ S đến A là
và OA là nửa đường chéo hình vuông đáy ABCD
Ta có : OA =
=> h = SO =
Vậy thể tích hình chóp S.ABCD là:
V = .Sđáy.h =
giải cơ ạ
An mê otp Dương Hùng.
· 4 tháng trước
ok nha
⋆˚࿔𝙪𝙮𝙚𝙣𝙣𝙝𝙞𝜗𝜚˚⋆
· 4 tháng trước
nhanh hộ mình với
Tính thể tích của hình chóp tứ giác đều S.ABCD
.
Thông tin được cung cấp trong bài toán
Hình chóp S.ABCD
là hình chóp tứ giác đều.
Cạnh đáy
𝐴𝐵=𝑎2√
.
Cạnh bên
𝑆𝐴=𝑎10√
.
Thông tin hữu ích
Thể tích hình chóp được tính bằng công thức V=13Bh
, với B
là diện tích đáy và
là chiều cao.
Đáy của hình chóp tứ giác đều là hình vuông.
Đường chéo của hình vuông cạnh xx
𝑥
là 𝑥2√
.
Trong hình chóp tứ giác đều, chân đường cao trùng với tâm của đáy.
Cách giải
Tìm diện tích đáy và chiều cao của hình chóp, sau đó áp dụng công thức tính thể tích.
Bước 1 . Tính diện tích đáy Bcap B
𝐵
:
Đáy là hình vuông cạnh 𝑎2√
.=(𝑎2√)2=2𝑎2
.Bước 2 . Tính chiều cao h
của hình chóp:
là tâm của đáy. SO
là chiều cao hh
ℎ
Đường chéo đáy
𝐴𝐶=𝐴𝐵2√=(𝑎2√)2√=2𝑎
.
AO=12AC=12(2a)
.
Áp dụng định lý Pytago trong tam giác vuông SOA
𝑆𝑂2=𝑆𝐴2−𝐴𝑂2
.
h2=(a10)2−a2=10a2−a2=9a2
.ℎ=9𝑎2√=3𝑎
.Bước 3 . Tính thể tích V
của hình chóp:
V=13Bh
V=13(2a2)(3a)=2a3
.Lời giải
Thể tích của hình chóp là 2a3
.
.
Thông tin được cung cấp trong bài toán
Hình chóp S.ABCD
là hình chóp tứ giác đều.
Cạnh đáy
𝐴𝐵=𝑎2√
.
Cạnh bên
𝑆𝐴=𝑎10√
.
Thông tin hữu ích
Thể tích hình chóp được tính bằng công thức V=13Bh
, với B
là diện tích đáy và
là chiều cao.
Đáy của hình chóp tứ giác đều là hình vuông.
Đường chéo của hình vuông cạnh xx
𝑥
là 𝑥2√
.
Trong hình chóp tứ giác đều, chân đường cao trùng với tâm của đáy.
Cách giải
Tìm diện tích đáy và chiều cao của hình chóp, sau đó áp dụng công thức tính thể tích.
Bước 1 . Tính diện tích đáy Bcap B
𝐵
:
Đáy là hình vuông cạnh 𝑎2√
.=(𝑎2√)2=2𝑎2
.Bước 2 . Tính chiều cao h
của hình chóp:
là tâm của đáy. SO
là chiều cao hh
ℎ
Đường chéo đáy
𝐴𝐶=𝐴𝐵2√=(𝑎2√)2√=2𝑎
.
AO=12AC=12(2a)
.
Áp dụng định lý Pytago trong tam giác vuông SOA
𝑆𝑂2=𝑆𝐴2−𝐴𝑂2
.
h2=(a10)2−a2=10a2−a2=9a2
.ℎ=9𝑎2√=3𝑎
.Bước 3 . Tính thể tích V
của hình chóp:
V=13Bh
V=13(2a2)(3a)=2a3
.Lời giải
Thể tích của hình chóp là 2a3
.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
10861
-
 Đã trả lời bởi chuyên gia
3934
Đã trả lời bởi chuyên gia
3934
Gửi báo cáo thành công!

 nha
nha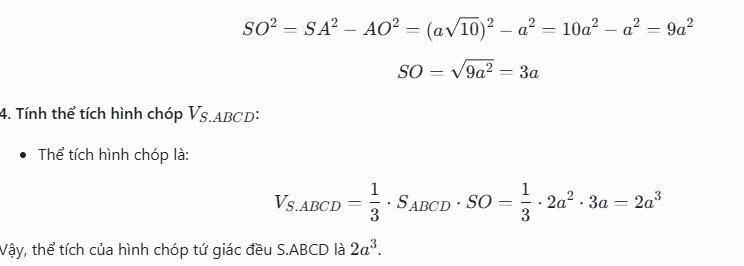 đc chưa
đc chưa

