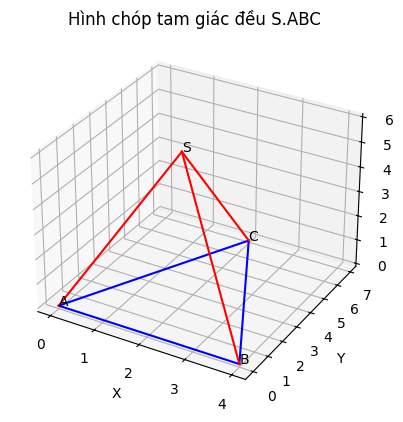
Bài 2: Cho hình chóp tam giác đều S.ABC với kích thước như hình vẽ.
a) Tính chu vi tam giác ABC .
b) Cho biết độ dài trung đoạn hình chóp S.ABC.
c) Tính diện tích xung quanh của hình chóp tam giác đều S.ABC.
Quảng cáo
3 câu trả lời 944
a) Tính chu vi tam giác ABC
Dữ kiện: Tam giác ABC đều, tức là ba cạnh AB, BC, và CA đều bằng nhau.
Công thức chu vi: Chu vi = 3×cạnh
+ Nếu độ dài cạnh đáy AB = BC = CA = a, thì chu vi tam giác ABC là: 3a
b, Độ dài trung đoạn của hình chóp
Trung đoạn của hình chóp tam giác đều là đoạn thẳng vuông góc với đáy và đi qua trọng tâm của đáy.
Công thức tính trung đoạn: d =
Phân tích đề bài và hình vẽ:
Hình chóp S.ABC là hình chóp tam giác đều. Điều này có nghĩa là:
Đáy ABC là một tam giác đều.
Các cạnh bên SA, SB, SC bằng nhau.
Hình chiếu của đỉnh S xuống mặt phẳng đáy trùng với tâm của tam giác đều ABC.
Dựa vào hình vẽ, ta có các kích thước sau:
Cạnh đáy (cạnh của tam giác ABC) là 4 cm.
Cạnh bên SA = 5 cm.
Có một đoạn thẳng từ S đến trung điểm của một cạnh đáy, ký hiệu là SM, với M là trung điểm của BC. Đoạn SM này chính là trung đoạn của hình chóp.
a) Tính chu vi tam giác ABC
Vì tam giác ABC là tam giác đều, nên tất cả ba cạnh đều bằng nhau và có độ dài là 4 cm. Chu vi của tam giác ABC là tổng độ dài ba cạnh. PABC=AB+BC+CA=4+4+4=3×4=12 cm.
Đáp số: Chu vi tam giác ABC là 12 cm.
b) Cho biết độ dài trung đoạn hình chóp S.ABC
Trung đoạn của hình chóp tam giác đều là đoạn thẳng nối đỉnh S với trung điểm của một cạnh đáy. Dựa vào hình vẽ, ta có thể thấy trung đoạn là SM. Để tính độ dài trung đoạn SM, ta xét tam giác SBC.
Tam giác SBC là tam giác cân tại S (vì SB = SC = 5 cm).
M là trung điểm của BC.
Do đó, SM là đường trung tuyến đồng thời là đường cao của tam giác SBC. Suy ra SM⊥BC. Xét tam giác vuông SMB:
SB=5 cm
BM=21BC=21×4=2 cm Áp dụng định lý Pytago trong tam giác vuông SMB, ta có: SM2+BM2=SB2 SM2+22=52 SM2+4=25 SM2=25−4=21 SM=21 cm.
Đáp số: Độ dài trung đoạn hình chóp S.ABC là 21 cm.
c) Tính diện tích xung quanh của hình chóp tam giác đều S.ABC
Diện tích xung quanh của hình chóp tam giác đều là tổng diện tích của ba mặt bên. Ba mặt bên là ba tam giác cân bằng nhau (SAB, SBC, SCA). Công thức tính diện tích xung quanh của hình chóp đều là: Sxq=21×chu vi đaˊy×độ daˋi trung đoạn
Chu vi đáy đã tính ở câu a): PABC=12 cm.
Độ dài trung đoạn đã tính ở câu b): SM=21 cm.
Thay số vào công thức: Sxq=21×12×21 =621 cm².
Đáp số: Diện tích xung quanh của hình chóp tam giác đều S.ABC là 621 cm².
Để tính chu vi tam giác ABC, chúng ta cần biết độ dài cạnh đáy của hình chóp tam giác đều S.ABC. Vì đây là hình chóp tam giác đều, nên tam giác ABC là tam giác đều.
Bước 1:
Xác định độ dài cạnh của tam giác ABC từ hình vẽ (nếu có). Giả sử độ dài cạnh đáy là 'a'.
Bước 2:
Áp dụng công thức tính chu vi tam giác đều: Chu vi = 3 * a.
b) Cho biết độ dài trung đoạn hình chóp S.ABC.
Trung đoạn của hình chóp đều là chiều cao của mặt bên (là tam giác cân) từ đỉnh đến cạnh đáy.
Bước 1:
Xác định trung đoạn từ thông tin hoặc hình vẽ đã cho. Giả sử trung đoạn là 'm'.
c) Tính diện tích xung quanh của hình chóp tam giác đều S.ABC.
Diện tích xung quanh của hình chóp đều bằng tổng diện tích các mặt bên.
Bước 1:
Tính diện tích một mặt bên. Vì các mặt bên là các tam giác cân bằng nhau, diện tích một mặt bên = (1/2) * cạnh đáy * trung đoạn = (1/2) * a * m.
Bước 2:
Tính diện tích xung quanh: Diện tích xung quanh = 3 * Diện tích một mặt bên = 3 * (1/2) * a * m = (3/2) * a * m.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
10861
-
 Đã trả lời bởi chuyên gia
3934
Đã trả lời bởi chuyên gia
3934



