Quảng cáo
4 câu trả lời 354
Đây là một bài toán nâng cao, nhưng có một cách giải rất hay mà học sinh lớp 6 có thể làm được.
Chúng ta sẽ biến đổi từng số hạng trong tổng S để tìm ra một quy luật mới.
Bước 1: Biến đổi mỗi số hạng
Ta có thể viết lại mỗi số hạng trong tổng S như sau:
1×3=1×(2+1)=1×2+1
2×4=2×(3+1)=2×3+2
3×5=3×(4+1)=3×4+3 ...
98×100=98×(99+1)=98×99+98
Bước 2: Phân tách tổng S thành hai tổng nhỏ hơn
Thay các số hạng đã biến đổi vào tổng S, ta được: S=(1×2+1)+(2×3+2)+⋯+(98×99+98)
Bây giờ, chúng ta sẽ nhóm các số hạng lại: S=(1×2+2×3+3×4+⋯+98×99)+(1+2+3+⋯+98)
Ta thấy, tổng S gồm hai phần:
Phần 1: Tổng của các tích hai số tự nhiên liên tiếp.
Phần 2: Tổng của các số tự nhiên từ 1 đến 98.
Bước 3: Tính từng phần
1. Tính Phần 2: 1+2+3+⋯+98 Đây là tổng của một dãy số tự nhiên. Chúng ta có thể dùng công thức: Tổng=2So^ˊcuo^ˊi×(So^ˊcuo^ˊi+1) Pha^ˋn2=298×(98+1)=298×99=49×99=4851
2. Tính Phần 1: 1×2+2×3+3×4+⋯+98×99 Đây là một dạng tổng đặc biệt. Ta có công thức giải nhanh là: Tổng=3So^ˊcuo^ˊi×(So^ˊcuo^ˊi+1)×(So^ˊcuo^ˊi+2) Áp dụng cho dãy số này (với số cuối là 98): Pha^ˋn1=398×(98+1)×(98+2)=398×99×100=98×33×100=323400
Bước 4: Cộng hai kết quả để tìm tổng S S=Pha^ˋn1+Pha^ˋn2=323400+4851=328251
Vậy, kết quả của phép tính là 328251.
𝑆=𝐴+𝐵=323400+4851=328251
Kết luận:
𝑆=328251
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Điền vào chỗ trống trong bảng thanh toán sau:
Số thứ tự Loại hàng Số lượng (quyển) Giá đơn vị (đồng) Tổng số tiền (đồng) 1 Vở loại 1 35 2000 ... 2 Vở loại 2 42 1500 ... 3 Vở loại 3 38 1200 ... Cộng: ... 170023 -
78717
-
35452
-
32348

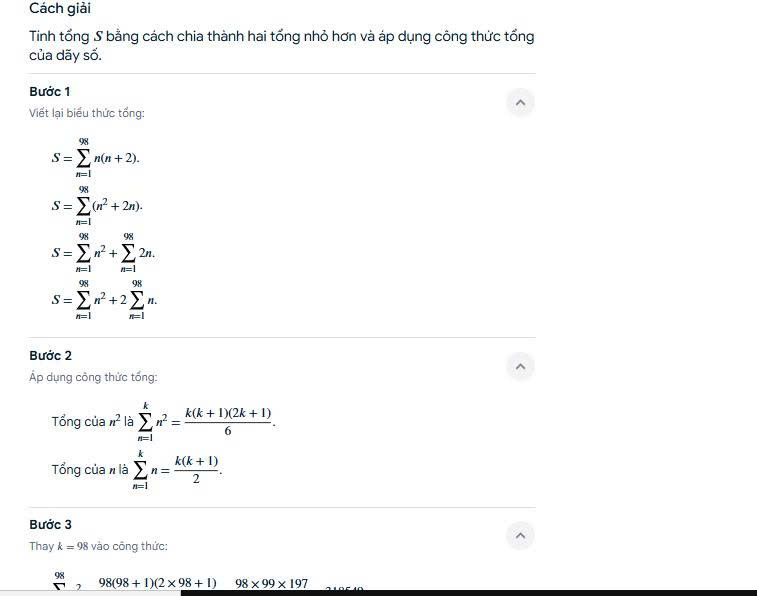 chưa
chưa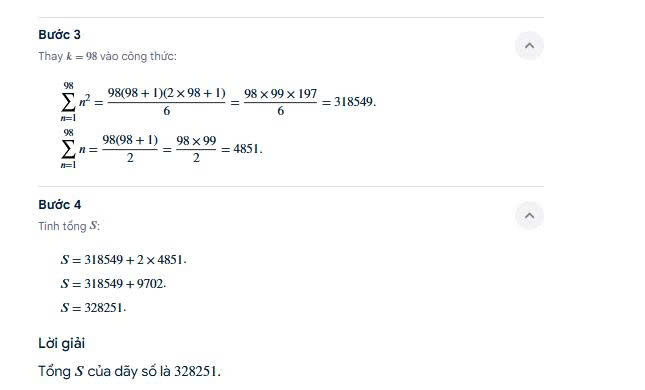 nek
nek 



