Quảng cáo
4 câu trả lời 148
Số cây trồng tỉ lệ thuận với số học sinh.
Gọi số cây 3 lớp trồng là \(x, y, z\) tương ứng.
Tổng tỉ lệ = 30 + 33 + 36 = 99
Số cây mỗi lớp
- 7A: \( \dfrac{30}{99} \times 33 = 10\) cây
- 7B: \( \dfrac{33}{99} \times 33 = 11\) cây
- 7C: \( \dfrac{36}{99} \times 33 = 12\) cây
Kết quả:
- Lớp 7A trồng 10 cây
- Lớp 7B trồng 11 cây
- Lớp 7C trồng 12 cây
Phần hình học: Chứng minh bất đẳng thức
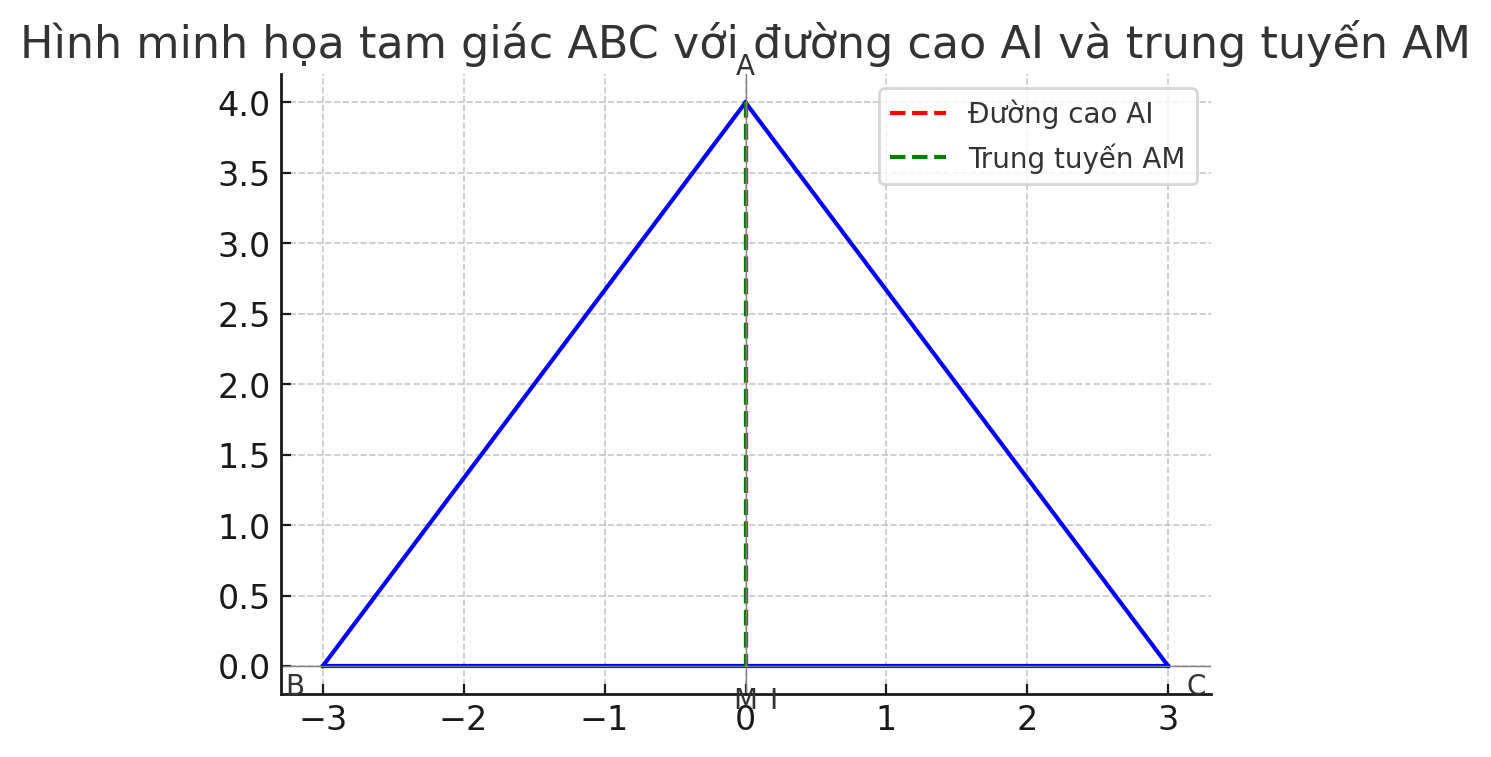
Cho tam giác ABC, AI là đường cao, AM là trung tuyến từ A.
Câu a: Chứng minh \(AI < \dfrac{1}{2}(AB + AC)\)
Ta sử dụng bất đẳng thức tam giác trong ∆ABI và ∆ACI:
Trong tam giác ABI: \(AI + IB > AB \Rightarrow AI > AB - IB\)
Tuy nhiên để chứng minh, ta sử dụng tính chất hình học:
- Trong tam giác, đường cao luôn nhỏ hơn cạnh đối diện → \(AI < AB\), \(AI < AC\)
- Do đó:
\[
AI < \min(AB, AC) < \dfrac{1}{2}(AB + AC)
\]
Câu b: Chứng minh \(AM < \dfrac{1}{2}(AB + AC)\)
Ta biết:
- M là trung điểm của BC ⇒ AM là trung tuyến
- Trong bất kỳ tam giác nào, độ dài trung tuyến*nhỏ hơn nửa tổng hai cạnh còn lại
\[
AM < \dfrac{1}{2}(AB + AC)
\]
Vậy
- a) \(AI < \dfrac{1}{2}(AB + AC)\)
- b) \(AM < \dfrac{1}{2}(AB + AC)\)
Bài 1 – Trồng cây:
Tỉ lệ học sinh: 30 : 33 : 36 → rút gọn: 10 : 11 : 12
Tổng cây: 33 cây
→ Mỗi lớp trồng:
- 7A: 10 cây
- 7B: 11 cây
- 7C: 12 cây
Bài 2 – Hình học:
Cho tam giác ABC, từ đỉnh A có:
- AI: đường cao
- AM: đường trung tuyến
a) AI < (AB+AC) vì đường cao nhỏ hơn hai cạnh → nhỏ hơn trung bình cộng.
b) AM < (AB+AC) vì trung tuyến nhỏ hơn trung bình cộng hai cạnh.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
52850
-
Hỏi từ APP VIETJACK52680
-
39717
-
Hỏi từ APP VIETJACK37052


