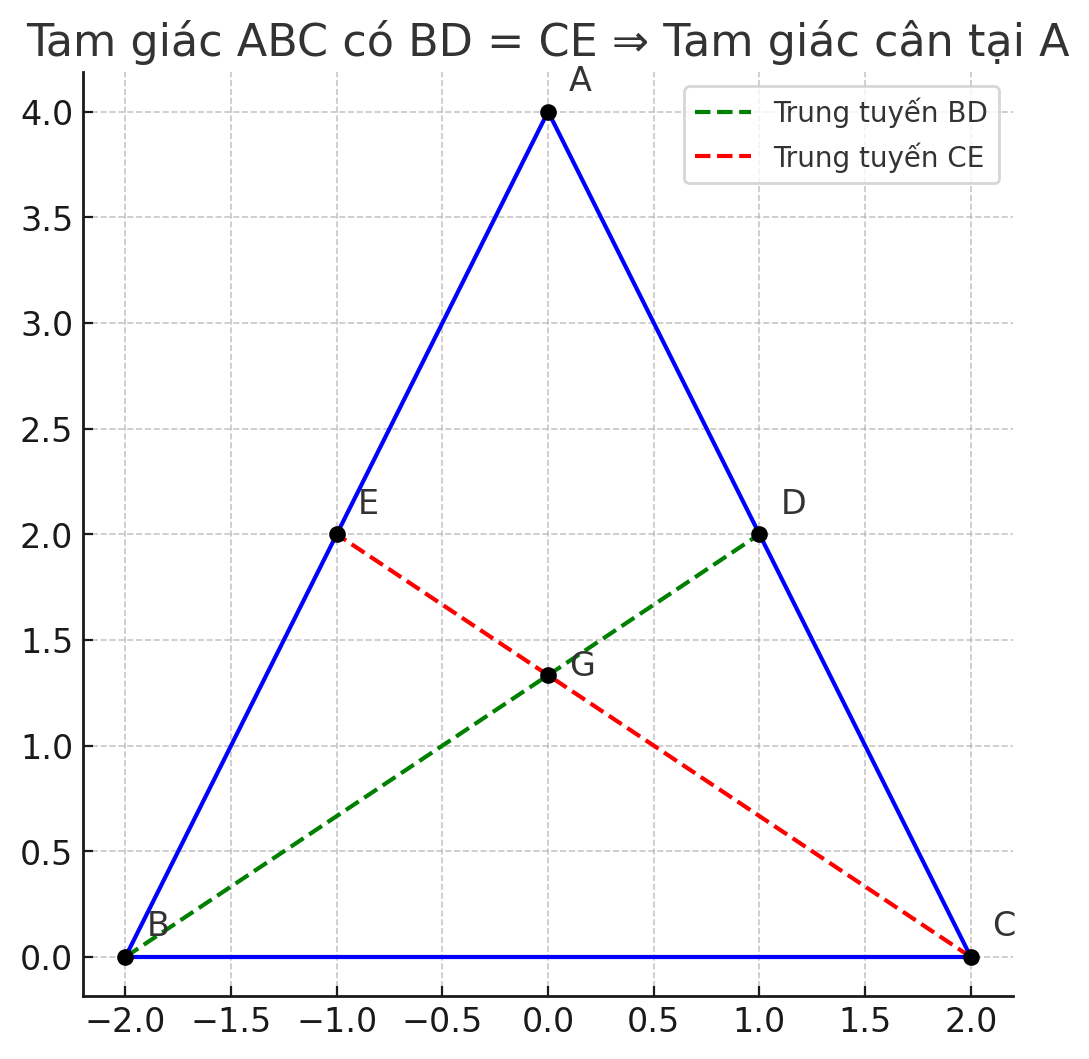
Toán bài 4 cho tam giác ABC có các đường trung tuyến BD và CE bằng nhau . Chứng minh rằng :ABC là Tam giác cân
Quảng cáo
2 câu trả lời 230
Gọi G là trọng tâm tam giác ABC (G là giao điểm các đường trung tuyến)
Vì G là trọng tâm, nên ta có:
\[
\begin{cases}
\vec{BG} = \frac{2}{3}\vec{BD} \\
\vec{CG} = \frac{2}{3}\vec{CE}
\end{cases}
\]
Vì BD = CE ⇒ \( |\vec{BD}| = |\vec{CE}| \)
⇒ \( |\vec{BG}| = |\vec{CG}| \)
⇒ Tam giác BGC có BG = CG
⇒ Tam giác BGC cân tại G ⇒ \( \angle GBG = \angle GCG \)
Xét tam giác ABC, có 2 đường trung tuyến bằng nhau ⇒ tam giác ABC cân tại A
Tam giác ABC cân tại A (AB = AC)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
74782
Đã trả lời bởi chuyên gia
74782 -
 Đã trả lời bởi chuyên gia
61046
Đã trả lời bởi chuyên gia
61046 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
53894
Đã trả lời bởi chuyên gia
53894 -
53022
-
 Đã trả lời bởi chuyên gia
40500
Đã trả lời bởi chuyên gia
40500 -
40009
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
37794
Đã trả lời bởi chuyên gia
37794 -
 Đã trả lời bởi chuyên gia
34564
Đã trả lời bởi chuyên gia
34564
Gửi báo cáo thành công!



