Giải thích các bước giải:

a.Ta có C∈(O),ABC∈(O),AB là đường kính →AC⊥BC→AC⊥BC 

Vì DA,DC, EC,EB là tiếp tuyến của (O)
→DA=DC,EC=EB→AD+BE=DC+CE+DE→DA=DC,EC=EB→AD+BE=DC+CE+DE

b.Ta có : DA,DCDA,DC là tiếp tuyến của (O)
→DA⊥OA,DC⊥OC→D,A,C,O→DA⊥OA,DC⊥OC→D,A,C,O cùng thuộc một đường tròn

Lại có OD⊥AC→ˆCAB=ˆADO(+ˆDOA=90o)OD⊥AC→CAB^=ADO^(+DOA^=90o)

c.Ta có : CECD=BEAD=IEIA→CI//ADCECD=BEAD=IEIA→CI//AD

→CIAD=CEEDKBBA=IKDA→CIAD=CEEDKBBA=IKDA

→IC=IK→IC=IK

d.Ta có :
AF⊥BD→ΔADB∼ΔBAN(g.g)AF⊥BD→ΔADB∼ΔBAN(g.g)

Mà M là trung điểm NB, O là trung điểm AB

→ΔDAO∼ΔABM→ΔDAO∼ΔABM

→ˆMAB=ˆADO=ˆCAB→A,C,M→MAB^=ADO^=CAB^→A,C,M thẳng hàng

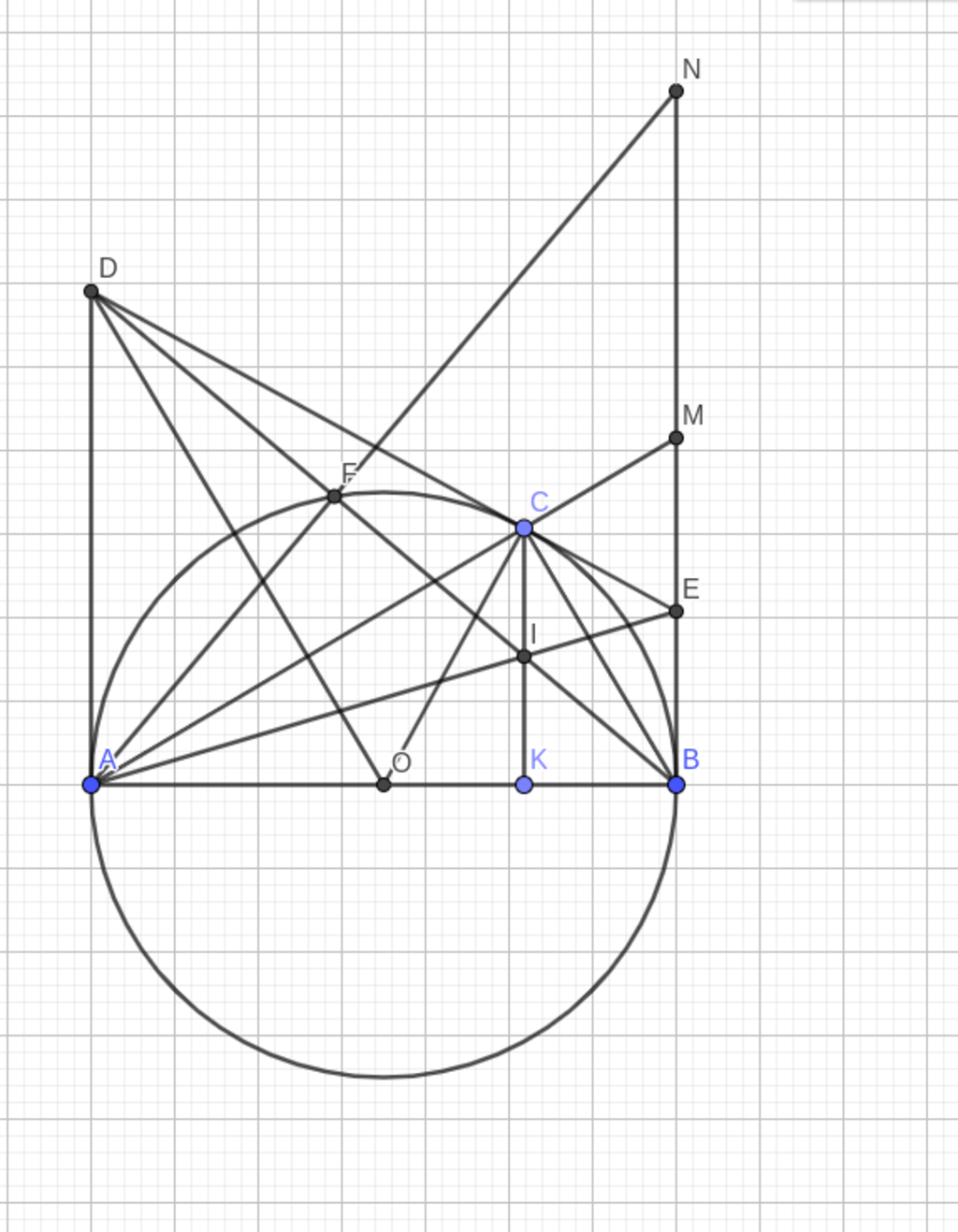
Xét tứ giác BHED, ta cần chứng minh rằng tổng hai góc đối diện của tứ giác này bằng 180 độ.
Gọi góc BHE và góc BDE. Ta có:

Góc BHE = góc BHC (vì H nằm trên BC và BC là dây cung)
Góc BDE = góc BDC (vì D nằm trên tiếp tuyến Bx)
Theo định lý tiếp tuyến và dây cung, ta có:

Góc BHC = góc BAC (góc tạo bởi dây cung AC)
Góc BDC = góc BOC (góc tạo bởi đường kính AB)
Vì AB là đường kính, nên góc BOC = 90 độ.
Suy ra tổng hai góc: Góc BHE + góc BDE = góc BAC + góc BOC = góc BAC + 90 độ.
Do AC < BC, góc BAC < 90 độ, nên tổng góc BHE + góc BDE = 90 độ + góc BAC = 180 độ.
Kết luận: Tứ giác BHED là tứ giác nội tiếp.