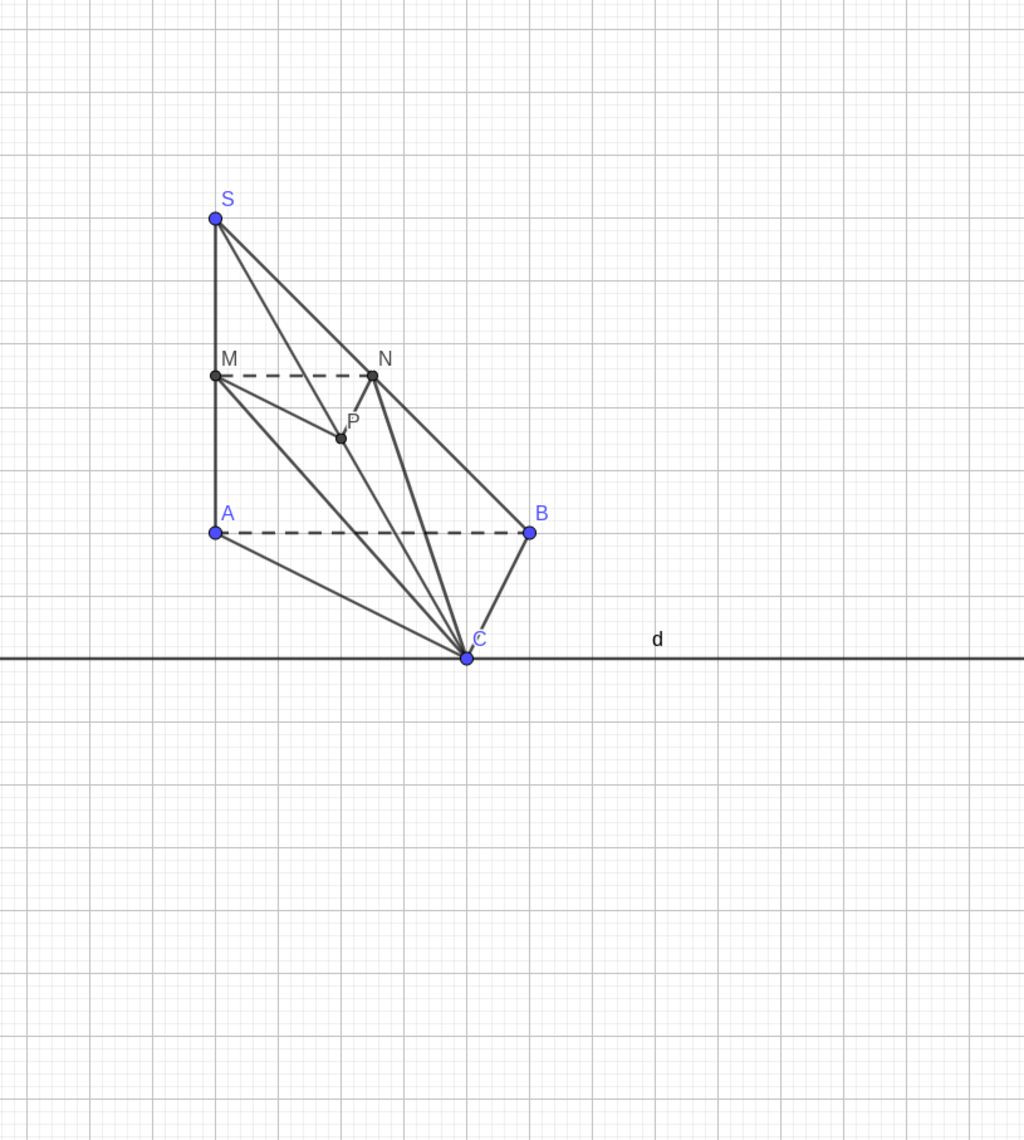
Để giải bài toán hình học về hình chóp S.ABC với các điểm M, N, P là các trung điểm của SA, SB, và SC, ta lần lượt thực hiện các yêu cầu a, b, c như sau:

### a) Tìm giao tuyến của hai mặt phẳng (ABC) và (MNC):

**Giả sử:**
- M là trung điểm của SA, tức là \( M = \frac{S + A}{2} \)
- N là trung điểm của SB, tức là \( N = \frac{S + B}{2} \)
- C là điểm trên mặt phẳng đáy ABC.

**Cách tìm giao tuyến:**
Giao tuyến giữa hai mặt phẳng (ABC) và (MNC) liên quan đến việc xác định phương trình của cả hai mặt phẳng.

- **Mặt phẳng (ABC)**: Mặt phẳng đi qua 3 điểm A, B, C có thể được biểu diễn qua phương trình tổng quát.

- **Mặt phẳng (MNC)**: Mặt phẳng đi qua các điểm M, N, C cũng có thể được biểu diễn tương tự.

Hai mặt phẳng sẽ giao nhau theo một đường thẳng nếu hệ số điều kiện của chúng không đồng nhất và chúng không song song với nhau.

### b) Chứng minh MN // (ABC):

Để chứng minh MN // (ABC), ta sử dụng tính chất cụ thể của các trung điểm và các mặt phẳng:

1. **Các điểm M và N** nằm trên đoạn thẳng SA và SB, tức là chúng tạo thành một đoạn thẳng nằm trong mặt phẳng (SAB).
2. Từ M và N, vẽ đường thẳng MN. Do M và N là trung điểm, khoảng cách giữa chúng thể hiện chiều dài đoạn thẳng MN là đoạn nối hai điểm trung điểm.
3. Suy ra, mặt phẳng (MNC) sẽ không cắt mặt phẳng (ABC) bất kỳ một điểm nào, mà VN sẽ song song với mặt phẳng đã nêu vì chúng đồng phẳng và có khả năng song song với mặt phẳng đáy ABC.

### c) Chứng minh (MNP) // (ABC):

1. **Điểm P** nằm trên đoạn SC, với P là trung điểm của SC.
2. Mặt phẳng (MNP) sẽ chứa các điểm M, N và P.
3. Biểu thức tương tự cho tính chất đoạn thẳng MN và chiều dài đoạn MP cũng cho ta thấy rằng M, N và P đều nằm trong một mặt phẳng song song với đáy ABC.
4. Do vậy, mặt phẳng (MNP) sẽ song song với mặt phẳng (ABC).

### Kết luận:
- Đoạn MN được thiết lập là song song với (ABC) từ vị trí và tính chất của các điểm trung điểm.
- Mọi đường thẳng trong (MNP) đều song song với mặt phẳng (ABC), và điều này khẳng định rằng (MNP) cũng là một mặt phẳng song song với mặt phẳng đáy của hình chóp S.ABC.