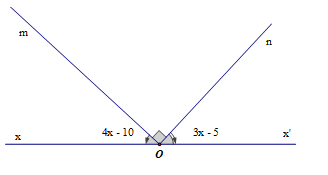
cho góc bẹt xoy trên cùng 1 nửa mặt phẳng bờ xy. Vẽ tia oa ob oc loa là tia phân giác của xob.ob là tia phân giác của xọc, tia oc là tia phân giác của yob. Tính xoa (vẽ hình giúp mk nha)
Quảng cáo
2 câu trả lời 512
Để tính góc \( x_{OA} \) tại điểm \( O \), chúng ta sẽ sử dụng định nghĩa của các tia phân giác và một số tính chất hình học.
Giả sử:
- Góc \( \angle xOB = \alpha \)
- Góc \( \angle yOC = \beta \)
- Góc \( \angle zOA = \theta \)
Chúng ta có các tia phân giác như sau:
- Tia \( OA \) là tia phân giác của góc \( \angle xOB \), nghĩa là:
\[
\angle xOA = \frac{\alpha}{2}
\]
- Tia \( OB \) là tia phân giác của góc \( \angle xOC \), nghĩa là:
\[
\angle xOB = \angle yOB = \frac{\theta}{2}
\]
- Tia \( OC \) là tia phân giác của góc \( \angle yOB \), nghĩa là:
\[
\angle yOC = \frac{\beta}{2}
\]
Vì các góc này nằm trong nửa mặt phẳng bờ \( xy \) và hình thành từ góc bẹt, ta có thể viết:
\[
\alpha + \beta + \theta = 180^\circ
\]
Cuối cùng, để tính \( x_{OA} \), chúng ta nhận thấy rằng \( OA \) phân chia góc \( xOB \) và góc \( yOC \). Nếu chúng ta xem xét tổng ba góc:
\[
\angle yOC + \angle yOB + \angle xOB = 180^\circ
\]
Như vậy:
1. \( \angle xOA = \frac{\alpha + \beta}{2} \)
2. Do đó, \( x_{OA} = \frac{\alpha + \beta}{2} \)
Vì chúng ta không có các giá trị cụ thể cho \( \alpha \) và \( \beta \), cũng như không có số lượng cụ thể cho \( x_{OA} \), nên bạn cần cung cấp thêm thông tin để thực hiện tính toán chính xác hơn.
Nếu bạn có các giá trị cụ thể hoặc mối quan hệ giữa các góc này, vui lòng cung cấp để tôi có thể trợ giúp bạn tốt hơn!
Sửa đề: Ob là tia phân giác của góc aOc
Oa là phân giác của góc xOb
=>góc xOa=1/2*góc xOb=góc aOb
Ob là phân giác của góc aOc
=>góc aOb=góc bOc
Oc là phân giác của góc bOy
=>góc bOc=góc yOc
=>góc xOa=góc aOb=góc bOc=góc cOy
mà góc xOa+góc aOb+góc bOc+góc cOy=180 độ
nên góc xOa=180 độ/4=45 độ
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11452
Đã trả lời bởi chuyên gia
11452 -
 Đã trả lời bởi chuyên gia
8620
Đã trả lời bởi chuyên gia
8620 -
 Đã trả lời bởi chuyên gia
5846
Đã trả lời bởi chuyên gia
5846