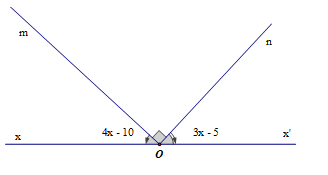
Bài 1. Cho hình vẽ
̂̂
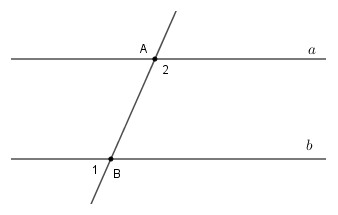
a) Biết𝐴 =53°,𝐵 =127°.CM:a//b
b)
c)
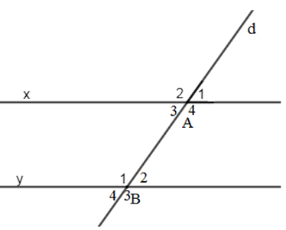
41 ̂̂̂
Biết 𝐵3 = 135°, 𝐴1 = 3𝐴4. CM a//b ̂̂̂
Biết𝐵3 −𝐵2 =50°,𝐴3 =115°.CM:a//b ̂̂̂
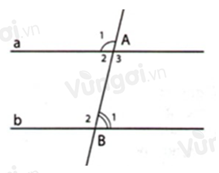
d) Biết𝐴 +𝐴 =240°,𝐵 =120°.CM:a//b
131
( Làm bằng 2 cách: cách 1 - so le trong, cách 2 - đồng vị)
Quảng cáo
2 câu trả lời 169
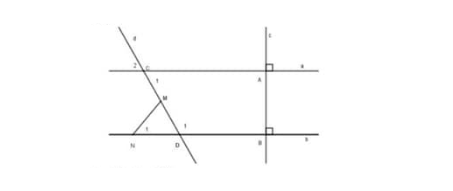
câu a
Để chứng minh rằng hai đường thẳng \(a\) và \(b\) song song dựa vào các góc đã cho, chúng ta cần xác định các góc liên quan đến hai đường thẳng và áp dụng định lý về các góc với hai đường thẳng song song.
**Giả sử:**
- Góc \(A = 53^\circ\)
- Góc \(B = 127^\circ\)
Chúng ta cần chứng minh \(a \parallel b\). Để làm điều này, hãy phân tích các góc \(A\) và \(B\) và kiểm tra các điều kiện liên quan đến hai đường thẳng song song.
### 1. Xác định loại góc dựa trên thông tin được cho
Thông thường, trong một bài toán như vậy, góc \(A\) và góc \(B\) có thể là các góc đồng vị, góc trong cùng phía, hoặc góc ngoài liên quan đến hai đường thẳng bị cắt bởi một đường thẳng thứ ba.
#### Tình huống thông thường:
- **Góc đồng vị:** Nếu hai đường thẳng song song bị cắt bởi một đường thẳng, các góc đồng vị sẽ bằng nhau.
- **Góc trong cùng phía:** Nếu hai đường thẳng song song bị cắt bởi một đường thẳng, tổng của các góc trong cùng phía bằng \(180^\circ\).
### 2. Xác định mối quan hệ giữa các góc
- **Góc trong cùng phía:** Tổng của hai góc trong cùng phía trên cùng một phía của đường cắt là \(180^\circ\).
Kiểm tra xem tổng của các góc \(A\) và \(B\) có bằng \(180^\circ\) không:
\[
A + B = 53^\circ + 127^\circ = 180^\circ
\]
### 3. Kết luận
Từ việc tính tổng của các góc \(A\) và \(B\) bằng \(180^\circ\), chúng ta có thể kết luận rằng các góc này là góc trong cùng phía trên cùng một phía của đường cắt. Theo định lý về góc trong cùng phía, nếu tổng của hai góc trong cùng phía là \(180^\circ\), thì hai đường thẳng bị cắt bởi một đường thẳng thứ ba là song song.
### Kết luận
Hai đường thẳng \(a\) và \(b\) là song song (\(a \parallel b\)) vì tổng của góc \(A = 53^\circ\) và góc \(B = 127^\circ\) là \(180^\circ\), chứng tỏ rằng chúng là các góc trong cùng phía và do đó, \(a \parallel b\).
câu a
Để chứng minh rằng hai đường thẳng aa và bb song song dựa vào các góc đã cho, chúng ta cần xác định các góc liên quan đến hai đường thẳng và áp dụng định lý về các góc với hai đường thẳng song song.
**Giả sử:**
- Góc A=53∘A=53∘
- Góc B=127∘B=127∘
Chúng ta cần chứng minh a∥ba∥b. Để làm điều này, hãy phân tích các góc AA và BB và kiểm tra các điều kiện liên quan đến hai đường thẳng song song.
### 1. Xác định loại góc dựa trên thông tin được cho
Thông thường, trong một bài toán như vậy, góc AA và góc BB có thể là các góc đồng vị, góc trong cùng phía, hoặc góc ngoài liên quan đến hai đường thẳng bị cắt bởi một đường thẳng thứ ba.
#### Tình huống thông thường:
- **Góc đồng vị:** Nếu hai đường thẳng song song bị cắt bởi một đường thẳng, các góc đồng vị sẽ bằng nhau.
- **Góc trong cùng phía:** Nếu hai đường thẳng song song bị cắt bởi một đường thẳng, tổng của các góc trong cùng phía bằng 180∘180∘.
### 2. Xác định mối quan hệ giữa các góc
- **Góc trong cùng phía:** Tổng của hai góc trong cùng phía trên cùng một phía của đường cắt là 180∘180∘.
Kiểm tra xem tổng của các góc AA và BB có bằng 180∘180∘ không:
A+B=53∘+127∘=180∘A+B=53∘+127∘=180∘
### 3. Kết luận
Từ việc tính tổng của các góc AA và BB bằng 180∘180∘, chúng ta có thể kết luận rằng các góc này là góc trong cùng phía trên cùng một phía của đường cắt. Theo định lý về góc trong cùng phía, nếu tổng của hai góc trong cùng phía là 180∘180∘, thì hai đường thẳng bị cắt bởi một đường thẳng thứ ba là song song.
### Kết luận
Hai đường thẳng aa và bb là song song (a∥ba∥b) vì tổng của góc A=53∘A=53∘ và góc B=127∘B=127∘ là 180∘180∘, chứng tỏ rằng chúng là các góc trong cùng phía và do đó, a∥ba∥b.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11452
Đã trả lời bởi chuyên gia
11452 -
 Đã trả lời bởi chuyên gia
8620
Đã trả lời bởi chuyên gia
8620 -
 Đã trả lời bởi chuyên gia
5846
Đã trả lời bởi chuyên gia
5846