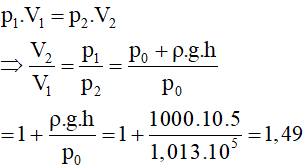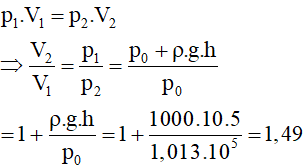khối lượng riêng của nước là 1000kg/m^3, gia tốc trọng trường g = 10m/s^2, áp suất khí quyển Po = 10^4 Pa)
A. tăng lên 3 lần. B. giảm đi 1,5 lần.
C. giảm đi 3 lần.
D. tăng lên 1,5 lần
Quảng cáo
4 câu trả lời 783
Để xác định thể tích của bọt khí tăng lên bao nhiêu lần khi nó nổi từ đáy hồ lên mặt nước, chúng ta cần sử dụng định luật Boyle-Mariotte (đối với trường hợp khí lý tưởng) và điều kiện áp suất khí quyển.
**Dữ liệu:**
- Độ sâu của hồ: \( h = 5 \, \text{m} \)
- Khối lượng riêng của nước: \( \rho = 1000 \, \text{kg/m}^3 \)
- Gia tốc trọng trường: \( g = 10 \, \text{m/s}^2 \)
- Áp suất khí quyển: \( P_0 = 10^4 \, \text{Pa} \)
**Áp suất tại đáy hồ:**
Áp suất tại đáy hồ \( P_1 \) được tính bằng tổng của áp suất khí quyển và áp suất do cột nước tạo ra:
\[
P_1 = P_0 + \rho g h
\]
Thay các giá trị vào:
\[
P_1 = 10^4 + 1000 \times 10 \times 5 = 10^4 + 50000 = 60000 \, \text{Pa}
\]
**Áp suất tại mặt nước:**
Áp suất tại mặt nước \( P_2 \) chỉ là áp suất khí quyển:
\[
P_2 = P_0 = 10^4 \, \text{Pa}
\]
**Sử dụng định luật Boyle-Mariotte:**
Định luật Boyle-Mariotte phát biểu rằng:
\[
P_1 V_1 = P_2 V_2
\]
Trong đó:
- \( V_1 \) là thể tích của bọt khí ở đáy hồ.
- \( V_2 \) là thể tích của bọt khí ở mặt nước.
Tìm tỷ lệ giữa \( V_2 \) và \( V_1 \):
\[
\frac{V_2}{V_1} = \frac{P_1}{P_2} = \frac{60000}{10000} = 6
\]
**Kết luận:**
Thể tích của bọt khí đã tăng lên 6 lần khi nó nổi từ đáy hồ lên mặt nước.
Vì vậy, câu trả lời đúng là không có trong các tùy chọn đưa ra, tuy nhiên nếu đây là một lỗi trong bài toán hoặc có sự điều chỉnh, bạn có thể phải kiểm tra lại các điều kiện cụ thể hoặc thông tin khác.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
153203
-
110953
-
106707
-
71461