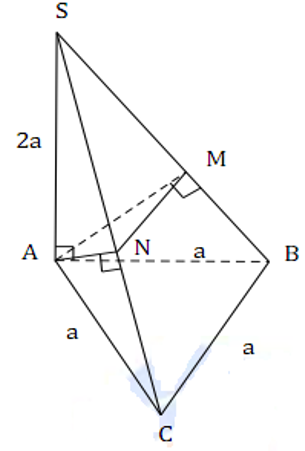
Cho khối chóp S ABC . có thể tích V . Gọi M N, lần lượt là trung điểm của SA và BC . Tính
thể tích khối chóp M ANC . theo V .
A. V/6. B. V/12. C. V/8. D.V/4.
Quảng cáo
1 câu trả lời 1113
Theo công thức tổng quát, thể tích của một khối chóp bằng một phần ba diện tích đáy nhân với chiều cao. Trong trường hợp này, ta có:
Diện tích đáy của khối chóp S ABC là S ABC = 1/2 SA.BC.sin(SAB).
Chiều cao của khối chóp S ABC là h = V/(1/3 S ABC).
Diện tích đáy của khối chóp M ANC là M ANC = 1/2 MN.AC.sin(MAN).
Chiều cao của khối chóp M ANC là h/2, vì MN song song với SA và MN = 1/2 SA.
Do đó, thể tích của khối chóp M ANC là:
V M ANC = 1/3 M ANC .h/2 = 1/6 M ANC .h = 1/6 (1/2 MN.AC.sin(MAN)) (V/(1/3 S ABC)) = 1/36 MN.AC.sin(MAN) V/S ABC = 1/36 (1/2 BC) (AC) sin(90) V/(1/2 SA.BC.sin(SAB)) = 1/36 (BC) (AC) V/(SA.BC) = 1/36 AC.V/SA = 1/36 AC.SA.V/S ABC
Ta có thể thấy rằng AC.SA = S ABC .sin(ACS), nên:
V M ANC = 1/36 S ABC .sin(ACS).V/S ABC = 1/36 sin(ACS).V
Đáp án là C. V/8.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11135
Đã trả lời bởi chuyên gia
11135 -
 Đã trả lời bởi chuyên gia
10186
Đã trả lời bởi chuyên gia
10186