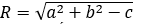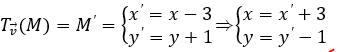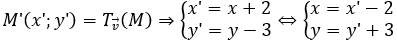Cách tìm ảnh của 1 đường tròn qua phép tịnh tiến cực hay
Với Cách tìm ảnh của 1 đường tròn qua phép tịnh tiến cực hay Toán học lớp 11 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách tìm ảnh của 1 đường tròn qua phép tịnh tiến cực hay.
Cách tìm ảnh của 1 đường tròn qua phép tịnh tiến cực hay
A. Phương pháp giải
- Nhắc lại Phương trình đường tròn: Trong mặt phẳng Oxy, phương trình đường tròn có dạng:
+ Dạng 1: Đương tròn (C) tâm I (a;b), bán kính R, (C): (x - a)2 + (y - b)2 = R2
+ Dạng 2: (C): x2 + y2 - 2ax - 2by + c = 0 (điều kiện: a2 + b2 - c > 0) khi đó đường tròn tâm I (a;b) và bán kính
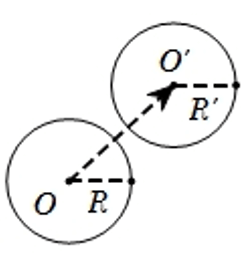
- Sử dụng tính chất: Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
→ Như vậy, để viết phương trình (C’) ta chỉ cần tìm ảnh tâm I của (C) qua phép tịnh tiến.
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn có phương trình (C): (x + 3)2 + (y – 1)2 = 4 với 

Hướng dẫn giải:
* Cách 1: (C) có tâm I(-3; 1) và bán kính R = 2
Khi đó: 

* Cách 2: Gọi M(x;y) ∈ (C),
Ta có: M ∈ (C) ⇔ (x’ + 3 + 3)2 + (y’ – 1 – 1)2 = 4 ⇔ M’ ∈ (C'): (x + 6)2 + (y – 2)2 = 4
Ví dụ 2: Trong mặt phẳng tọa độ Oxy ,Tìm ảnh của (C) qua phép tịnh tiến theo 

Hướng dẫn giải:
Cách 1. Sử dụng biểu thức tọa độ.
Lấy điểm M(x;y) tùy ý thuộc đường tròn (C), ta có x2 + y2 + 2x - 4y - 4 = 0 (*)
Gọi
Thay vào phương trình (*) ta được (x' - 2)2 + (y' + 3)2 + 2(x' - 2) - 4(y' + 3) - 4 = 0
⇔ x'2 + y'2 -2x' + 2y' - 7 = 0.
Vậy ảnh của (C) là đường tròn(C'): x2 + y2 - 2x + 2y - 7 = 0.
Cách 2. Sử dụng tính chất của phép tịnh tiến
Dễ thấy (C) có tâm I(-1;2) và bán kính r = 3. Gọi (C') = 
Ta có 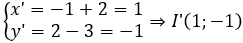
Ví dụ 3: Tìm tọa độ vectơ 

a) (C): (x – 2)2 + (y + 3)2 = 4 và (C’): (x + 5)2 + (y – 1)2 = 4
b) (C): x2 + y2 – 2x + 4y + 2 = 0 và (C’): x2 + y2 + 4x – 6y + 10 = 0
Hướng dẫn giải:
a) Từ (C), ta có: tâm I(2;-3) và từ (C’), ta có: tâm I’(-5; 1)
Khi đó: 

b) Từ (C), ta có: tâm I(1;-2) và từ (C’), ta có: tâm I’(-2; 3)
Khi đó: 


C. Bài tập trắc nghiệm
Câu 1. Trong mặt phẳng tọa độ Oxy, ảnh của đường tròn (C): (x + 1)2 + (y - 3)2 = 4 qua phép tịnh tiến theo vectơ 
A. (x + 2)2 + (y + 5)2 = 4.
B. (x - 2)2 + (y - 5)2 = 4.
C. (x - 1)2 + (y + 3)2 = 4.
D. (x + 4)2 + (y - 1)2 = 4.
Câu 2. Trong mặt phẳng Oxy, cho vectơ 

A. (C'): (x - 4)2 + (y - 1)2 = 4.
B. (C'): (x - 4)2 + (y - 1)2 = 9.
C. (C'): (x + 4)2 + (y + 1)2 = 9.
D. (C'): x2 + y2 + 8x + 2y - 4 = 0.
Câu 3. Cho 

A. x2 + y2 + 8x + 2y - 4 = 0
B. (x + 5)2 + (y - 4)2 = 9.
C. (x + 1)2 + y2 = 9.
D. (x - 5)2 + (y + 4)2 = 9.
Câu 4. Trong mặt phẳng tọa độ Oxy cho hai đường tròn (C1) và (C2) bằng nhau có phương trình lần lượt là (x - 1)2 + (y + 2)2 = 16 và (x + 3)2 + (y - 4)2 = 16. Giả sử T là phép tịnh tiến theo vectơ 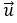
A. 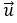
B. 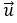
C. 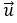
D. 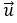
Câu 5. Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình x2 + y2 + 4x - 6y - 5 = 0. Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ 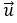

A. x2 + y2 - 18 = 0.
B. x2 + y2 - x + 8y + 2 = 0.
C. x2 + y2 + x - 6y - 5 = 0.
D. x2 + y2 - 4y - 4 = 0.
Câu 6. Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C): (x - 1)2 + (y + 2)2 = 9 và đường tròn(C'): (x + 1)2 + (y - 3)2 = 9. Phép tịnh tiến theo véc tơ 

A. 
B. 
C. 
D. 
Câu 7. Trong mặt phẳng Oxy, cho đường thẳng d có phương trình x + y - 1 = 0 và đường tròn (C): (x - 3)2 + (y - 1)2 = 1. Ảnh của đường thẳng d qua phép tịnh tiến theo véc tơ 
A. 5.
B. 8.
C. 6.
D. 7.
Câu 8. Trong mặt phẳng tọa độ Oxy, cho hai đường tròn (C): (x + m)2 + (y - 2)2 = 5 và (C'): x2 + y2 + 2(m - 2)y - 6x + 12 + m2 = 0. Vectơ 
A. 
B. 
C. 
D. 
Câu 9. Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?
A. 0
B. 1
C. 2
D. Vô số.
Câu 10. Cho đường tròn (C) có tâm O và đường kính AB. Gọi ∆ là tiếp tuyến của (C) tại điểm
A. Phép tịnh tiến theo vectơ 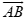
A. Đường kính của đường tròn (C) song song với ∆.
B. Tiếp tuyến của (C) tại điểm B.
C. Tiếp tuyến của (C) song song với AB.
D. Đường thẳng song song với ∆và đi qua O