Trắc nghiệm Toán 7 Bài 23: Đại lượng tỉ lệ nghịch
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 23: Đại lượng tỉ lệ nghịch có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 23.
Trắc nghiệm Toán 7 Bài 23: Đại lượng tỉ lệ nghịch - Kết nối tri thức
I. Nhận biết
Câu 1. Cho biết đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a ( a khác 0) . Hãy biểu diễn y theo x.
A. y = ;
B. y = –ax;
C. y = ax;
D. y = .
Đáp án: D
Giải thích:
Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a nên y liên hệ với x theo công thức y = với a khác 0.
Vậy đáp án đúng là D.
Câu 2. Chọn câu đúng. Nếu y = ( a khác 0 ) thì ta nói
A. y tỉ lệ nghịch với x theo hệ số tỉ lệ a;
B. y tỉ lệ thuận với x theo hệ số tỉ lệ a;
C. x tỉ lệ thuận với y theo hệ số tỉ lệ a;
D. Cả 3 đáp án trên đều sai.
Đáp án: A
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Vậy đáp án đúng là A.
Câu 3. Chọn câu đúng. Nếu y = thì ta nói
A. y tỉ lệ nghịch với x theo hệ số tỉ lệ 5;
B. y tỉ lệ thuận với x theo hệ số tỉ lệ 5;
C. y tỉ lệ nghịch với x theo hệ số tỉ lệ ;
D. Không kết luận được điều gì về x và y.
Đáp án: A
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Như vậy nếu đại lượng y liên hệ với đại lượng x theo công thức y = thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ 5.
Vậy chọn đáp án A.
Câu 4. Cho biết đại lượng x tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ –3. Hãy biểu diễn y theo x.
A. y = –3x;
B. y = ;
C. y = 3x;
D. y = x.
Đáp án: B
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Như vậy nếu đại lượng y liên hệ với đại lượng x theo công thức y = thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ –3.
Vậy chọn đáp án B.
Câu 5. Chọn câu đúng. Nếu y = thì ta nói:
A. y tỉ lệ nghịch với x theo hệ số tỉ lệ –2;
B. y tỉ lệ nghịch với x theo hệ số tỉ lệ –;
C. y tỉ lệ thuận với x theo hệ số tỉ lệ –;
D. y tỉ lệ thuận với x theo hệ số tỉ lệ –2.
Đáp án: A
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Như vậy nếu đại lượng y liên hệ với đại lượng x theo công thức y = thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ –2.
Vậy chọn đáp án A.
II. Thông hiểu
Câu 1. Biết rằng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 4. Tìm hệ số tỉ lệ.
A. 2;
B. 8;
C. 4;
D. 1.
Đáp án: B
Giải thích:
Do x và y tỉ lệ nghịch với nhau nên đại lượng y liên hệ với đại lượng x qua công thức
y = với a khác 0.
Theo đề bài khi x = 2 thì y = 4 nên thay vào công thức ta có 4 = hay a = 8.
Vậy x và y tỉ lệ nghịch với nhau với hệ số tỉ lệ là 8.
Câu 2. Biết rằng x và y tỉ lệ nghịch với nhau và khi x = 5 thì y = 4. Tìm giá trị tương ứng của y khi x = 4.
A. 8;
B. 6;
C. 3;
D. 5.
Đáp án: D
Giải thích:
Do x và y tỉ lệ nghịch với nhau nên đại lượng y liên hệ với đại lượng x qua công thức
y = với a khác 0.
Theo đề bài khi x = 5 thì y = 4 nên thay vào công thức ta có 4 = hay a = 20.
Ta được công thức y = . Khi x = 4 thì y = = 5.
Vậy khi x = 4 thì y = 5. Chọn đáp án D.
Câu 3. Cho x và y là hai đại lượng tỉ lệ nghịch. Gọi x1 , x2 là hai giá trị của x, gọi y1, y2 là hai giá trị của y. Biết 2x1 – 3y2 = 22 và y1 = 5, x2 = 2. Biểu diễn y theo x.
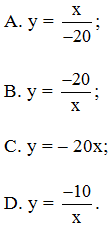
Đáp án: B
Giải thích:
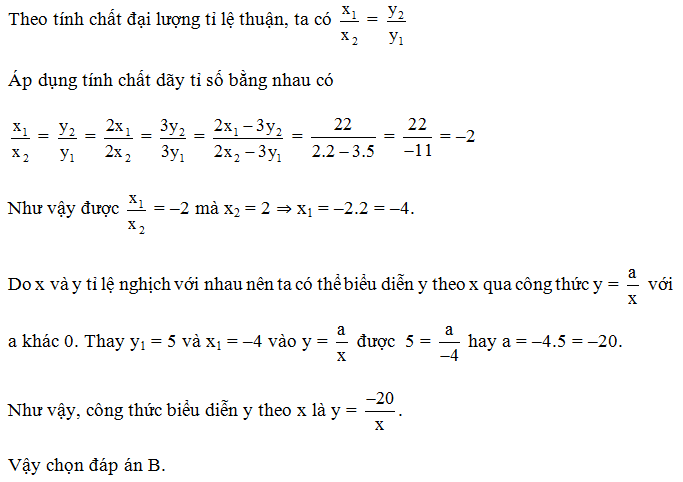
Câu 4. Cho x và y tỉ lệ nghịch và khi x = 3 thì y = 7. Biểu diễn y theo x.
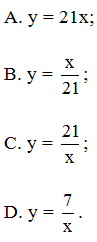
Đáp án: C
Giải thích:
Do x và y tỉ lệ nghịch với nhau nên ta có thể biểu diễn y theo x qua công thức y = với a khác 0. Thay y = 7 và x = 3 vào y = được 7 = hay a = 3.7 = 21.
Như vậy, công thức biểu diễn y theo x là y = .
Chọn đáp án C.
Câu 5. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ 4 và x tỉ lệ nghịch với z theo hệ số tỉ lệ . Chọn câu đúng
A. y tỉ lệ thuận với z theo hệ số tỉ lệ ;
B. y tỉ lệ thuận với z theo hệ số tỉ lệ ;
C. y tỉ lệ nghịch với z theo hệ số tỉ lệ ;
D. y tỉ lệ nghịch với z theo hệ số tỉ lệ .
Đáp án: B
Giải thích:
Do y tỉ lệ nghịch với x theo hệ số tỉ lệ 4 nên y = .
Do x tỉ lệ nghịch với z theo hệ số nên x = .
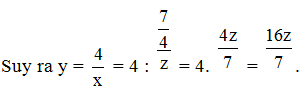
Như vậy y = . Ta nói y tỉ lệ thuận với z theo hệ số tỉ lệ .
Chọn đáp án B.
Câu 6. Cho y tỉ lệ nghịch với x theo hệ số tỉ lệ –20. Tìm giá trị tương ứng của y khi
x = 6.
A. ;
B. ;
C. ;
D. .
Đáp án: D
Giải thích:
Do y tỉ lệ nghịch với x theo hệ số tỉ lệ –20 nên ta có y = .
Khi x = 6 thì y = = .
Vậy y = . Chọn đáp án D.
Câu 7. Cho y thỉ lệ thuận với x theo hệ số tỉ lệ , x tỉ lệ nghịch với z theo hệ số tỉ lệ . Chọn câu đúng.
A. y tỉ lệ thuận với z theo hệ số tỉ lệ ;
B. y tỉ lệ nghịch với z theo hệ số tỉ lệ ;
C. y tỉ lệ nghịch với z theo hệ số tỉ lệ ;
D. y tỉ lệ thuận với z theo hệ số tỉ lệ .
Đáp án: B
Giải thích:

III. Vận dụng
Câu 1. Một xe máy chạy từ A đến B với vận tốc 30 km/h hết 3 giờ. Hỏi xe máy đó chạy từ A đến B với vận tốc 60 km/h sẽ hết bao nhiêu thời gian?
A. 1,15 giờ;
B. 1 giờ 30 phút;
C. 6 giờ;
D. 2 giờ 30 phút.
Đáp án: B
Giải thích:
Gọi thời gian xe máy đi từ A đến B với vận tốc 60 km/h là x ( giờ)
Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên:
30.3 = 60.x ⇒ x = = 1,5 giờ hay 1 giờ 30 phút.
Chọn đáp án B.
Câu 2. Với cùng 1 số tiền để mua 34 mét vải loại 1 có thể mua được bao nhiêu mét vải loại 2. Biết giá tiền 1 mét vải loại 2 chỉ bằng 85% giá tiền 1 mét vải loại 1.
A. 55;
B. 60;
C. 40;
D. 45.
Đáp án: C
Giải thích:
Gọi giá tiền của 1 mét vải loại 1 là x ( x > 0) và y là số mét vải loại 2 mua được ( k > 0).
Khi đó giá tiền của 1 mét vải loại 2 là 0,85x hay 85%x.
Với cùng 1 số tiền, giá tiền 1 mét vải và số mét vải mua được là hai đại lượng tỉ lệ nghịch nên ta có 34x = 0,85.x.k
⇒ k = = 40.
Vậy mua được 40 mét vải loại 2. Chọn đáp án C.
Câu 3. Một đơn vị thanh niên xung phong chuẩn bị một số gạo đủ cho đơn vị ăn trong 30 ngày. Sau 10 ngày đơn vị nhận thêm 10 người nữa. Hỏi số gạo còn lại đơn vị sẽ đủ ăn trong bao nhiêu ngày, biết lúc đầu đơn vị có 90 người ?
A. 20 ngày;
B. 15 ngày;
C. 16 ngày;
D. 14 ngày.
Đáp án: C
Giải thích:
Sau 10 ngày, còn lại số gạo đủ cho 90 người ăn trong 30 – 10 = 20 (ngày).
Sau khi thêm 10 người, đơn vị có 90 + 10 = 100 ( người)
Số gạo còn lại đủ cho 100 người ăn trong x ngày.
Với số gạo không đổi, số người ăn và số ngày ăn hết là hai đại lượng tỉ lệ nghịch. Ta có
100x = 90.20 ⇒ x = = 18.
Vậy sau khi thêm 10 người sau 10 ngày, số gạo còn lại đủ ăn trong 18 ngày nữa. Chọn đáp án C.
Các câu hỏi trắc nghiệm Toán 7 sách Kết nối tri thức có đáp án, chọn lọc khác:


