Đáp án đúng là: B

Phương pháp an toàn là dùng nước đá và nước đá khô.

Đáp án đúng là: C

- Dùng quỳ tím nhận biết được CH3COOH, HCOOH làm quỳ tím hóa đỏ, CH3CHO không làm quỳ tím đổi màu.

- Dùng dung dịch AgNO3/NH3 nhận được HCOOH, còn lại là CH3­COOH.

        HCOOH + 2AgNO3 + 4NH3 + H2O→ (NH4)2CO3 + 2Ag + 2NH4NO3

Những lọ măng, dưa chuột muối đó người ta đã ngâm trong giấm. Một số thức ăn, thường là rau quả được ngâm vào giấm và sau đó đóng vào chai kín. Giấm là dung dịch acetic acid nồng độ 2% - 5%, ngăn được sự phát triển của vi khuẩn nên thức ăn được bảo quản. Hành, măng và dưa chuột và một số loại khác là những thức ăn được ngâm giấm thường gặp.

Để giải bài toán này, ta sẽ thiết lập hệ phương trình dựa trên thông tin đề bài cung cấp. Gọi x𝑥 là giá tiền của một cái bút và y𝑦 là giá tiền của một quyển vở.

Ta có các phương trình sau dựa trên thông tin:

1. Dương mua 5 cái bút và 3 quyển vở hết 49 000 đồng:
5x+3y=490005𝑥+3𝑦=49000

2. Giang mua 3 cái bút và 2 quyển vở hết 31 000 đồng:
3x+2y=310003𝑥+2𝑦=31000

Bây giờ, chúng ta sẽ giải hệ phương trình này để tìm giá tiền của một cái bút x𝑥.

Bước 1: Nhân phương trình thứ hai với 3 và phương trình thứ nhất với 2 để làm hệ số của y𝑦 trong cả hai phương trình giống nhau:
3(3x+2y)=3(31000)⟹9x+6y=930003(3𝑥+2𝑦)=3(31000)⟹9𝑥+6𝑦=93000
2(5x+3y)=2(49000)⟹10x+6y=980002(5𝑥+3𝑦)=2(49000)⟹10𝑥+6𝑦=98000

Bước 2: Trừ phương trình mới thứ hai cho phương trình mới thứ nhất:
(10x+6y)−(9x+6y)=98000−93000(10𝑥+6𝑦)−(9𝑥+6𝑦)=98000−93000
x=5000𝑥=5000

Vậy giá tiền của một cái bút là 50005000 đồng.

Kiểm tra lại:
5x+3y=490005𝑥+3𝑦=49000
5(5000)+3y=490005(5000)+3𝑦=49000
25000+3y=4900025000+3𝑦=49000
3y=240003𝑦=24000
y=8000𝑦=8000

Và kiểm tra phương trình thứ hai:
3x+2y=310003𝑥+2𝑦=31000
3(5000)+2(8000)=310003(5000)+2(8000)=31000
15000+16000=3100015000+16000=31000

Cả hai phương trình đều đúng. Do đó, giá tiền của một cái bút là 50005000 đồng.

Đáp án đúng là @5000@5000 đồng.
 

Để giải bài toán này, ta sẽ thiết lập hệ phương trình dựa trên thông tin đề bài cung cấp. Gọi x𝑥 là giá tiền của một cái bút và y𝑦 là giá tiền của một quyển vở.

Ta có các phương trình sau dựa trên thông tin:

1. Dương mua 5 cái bút và 3 quyển vở hết 49 000 đồng:
5x+3y=490005𝑥+3𝑦=49000

2. Giang mua 3 cái bút và 2 quyển vở hết 31 000 đồng:
3x+2y=310003𝑥+2𝑦=31000

Bây giờ, chúng ta sẽ giải hệ phương trình này để tìm giá tiền của một cái bút x𝑥.

Bước 1: Nhân phương trình thứ hai với 3 và phương trình thứ nhất với 2 để làm hệ số của y𝑦 trong cả hai phương trình giống nhau:
3(3x+2y)=3(31000)⟹9x+6y=930003(3𝑥+2𝑦)=3(31000)⟹9𝑥+6𝑦=93000
2(5x+3y)=2(49000)⟹10x+6y=980002(5𝑥+3𝑦)=2(49000)⟹10𝑥+6𝑦=98000

Bước 2: Trừ phương trình mới thứ hai cho phương trình mới thứ nhất:
(10x+6y)−(9x+6y)=98000−93000(10𝑥+6𝑦)−(9𝑥+6𝑦)=98000−93000
x=5000𝑥=5000

Vậy giá tiền của một cái bút là 50005000 đồng.

Kiểm tra lại:
5x+3y=490005𝑥+3𝑦=49000
5(5000)+3y=490005(5000)+3𝑦=49000
25000+3y=4900025000+3𝑦=49000
3y=240003𝑦=24000
y=8000𝑦=8000

Và kiểm tra phương trình thứ hai:
3x+2y=310003𝑥+2𝑦=31000
3(5000)+2(8000)=310003(5000)+2(8000)=31000
15000+16000=3100015000+16000=31000

Cả hai phương trình đều đúng. Do đó, giá tiền của một cái bút là 50005000 đồng.

Đáp án đúng là @5000@5000 đồng.
 

A

Kiến thức: sự hòa hợp giữa các thì

B

Kiến thức: từ vựng

Giải thích:

establish somebody/something/yourself (in something) (as something): giữ vững vị trí

one of the + N (đếm được số nhiều)

Tạm dịch: Mike nhanh chóng giữ vững được vị trí là một trong những cầu thủ có giá trị nhất giải bóng đá quốc gia.
 

C

Kiến thức: cấp so sánh nhất

Giải thích:

Dạng so sánh nhất của tính từ “bad” là “worst”.

Tạm dịch: “Tại sao bạn lại lãng phí tiền đi xem bộ phim đó chứ?”

“Tôi biết. Đó là bộ phim tệ nhất tôi từng xem.”
 

### Câu 2: Giao điểm của Parabol và Đường thẳng

Cho parabol (P):y=x2(𝑃):𝑦=𝑥2 và đường thẳng d:y=2x+|m|+1𝑑:𝑦=2𝑥+|𝑚|+1.

#### a) Chứng minh đường thẳng d𝑑 luôn cắt (P)(𝑃) tại 2 điểm phân biệt.

Giao điểm của (P)(𝑃) và d𝑑 được xác định bằng cách giải hệ phương trình:

x2=2x+|m|+1𝑥2=2𝑥+|𝑚|+1

Chuyển tất cả các số hạng sang một vế để có phương trình bậc hai:

x2−2x−(|m|+1)=0𝑥2−2𝑥−(|𝑚|+1)=0

Để phương trình có hai nghiệm phân biệt, ta cần kiểm tra điều kiện của biệt thức (Δ):

Δ=b2−4acΔ=𝑏2−4𝑎𝑐

Với a=1𝑎=1, b=−2𝑏=−2, và c=−(|m|+1)𝑐=−(|𝑚|+1), ta có:

Δ=(−2)2−4⋅1⋅(−(|m|+1))Δ=(−2)2−4⋅1⋅(−(|𝑚|+1))

Δ=4+4(|m|+1)Δ=4+4(|𝑚|+1)

Δ=4+4|m|+4Δ=4+4|𝑚|+4

Δ=8+4|m|Δ=8+4|𝑚|

Vì Δ=8+4|m|Δ=8+4|𝑚| luôn lớn hơn 0 với mọi giá trị của m𝑚, nên phương trình x2−2x−(|m|+1)=0𝑥2−2𝑥−(|𝑚|+1)=0 luôn có hai nghiệm phân biệt.

Do đó, đường thẳng d𝑑 luôn cắt parabol (P)(𝑃) tại 2 điểm phân biệt.

#### b) Tìm m𝑚 để đường thẳng d𝑑 cắt (P)(𝑃) tại 2 điểm phân biệt có hoành độ x1,x2𝑥1,𝑥2 (với x1<x2𝑥1<𝑥2) thỏa mãn |x1⋅x2|+|x2|−|x1|=8|𝑥1⋅𝑥2|+|𝑥2|−|𝑥1|=8

Ta sử dụng nghiệm của phương trình bậc hai để tìm x1𝑥1 và x2𝑥2. 

Nghiệm của phương trình x2−2x−(|m|+1)=0𝑥2−2𝑥−(|𝑚|+1)=0 là:

x1,2=2±√8+4|m|2𝑥1,2=2±8+4|𝑚|2

x1,2=1±√2+|m|𝑥1,2=1±2+|𝑚|

Giả sử x1=1−√2+|m|𝑥1=1−2+|𝑚| và x2=1+√2+|m|𝑥2=1+2+|𝑚|.

Ta kiểm tra điều kiện thỏa mãn:

|x1⋅x2|+|x2|−|x1|=8|𝑥1⋅𝑥2|+|𝑥2|−|𝑥1|=8

Tính tích x1⋅x2𝑥1⋅𝑥2:

x1⋅x2=(1−√2+|m|)(1+√2+|m|)𝑥1⋅𝑥2=(1−2+|𝑚|)(1+2+|𝑚|)

x1⋅x2=12−(√2+|m|)2𝑥1⋅𝑥2=12−(2+|𝑚|)2

x1⋅x2=1−(2+|m|)𝑥1⋅𝑥2=1−(2+|𝑚|)

x1⋅x2=−1−|m|𝑥1⋅𝑥2=−1−|𝑚|

Tính giá trị tuyệt đối:

|x1⋅x2|=|−1−|m||=1+|m||𝑥1⋅𝑥2|=|−1−|𝑚||=1+|𝑚|

Tính giá trị tuyệt đối của x1𝑥1 và x2𝑥2:

|x2|=1+√2+|m||𝑥2|=1+2+|𝑚|

|x1|=|1−√2+|m|||𝑥1|=|1−2+|𝑚||

Có hai trường hợp:

1. Nếu 1≥√2+|m|1≥2+|𝑚|:

|x1|=1−√2+|m||𝑥1|=1−2+|𝑚|

2. Nếu 1<√2+|m|1<2+|𝑚|:

|x1|=√2+|m|−1|𝑥1|=2+|𝑚|−1

Trường hợp 1: 1≥√2+|m|1≥2+|𝑚|:

Tổng cộng:

|x1⋅x2|+|x2|−|x1|=(1+|m|)+(1+√2+|m|)−(1−√2+|m|)|𝑥1⋅𝑥2|+|𝑥2|−|𝑥1|=(1+|𝑚|)+(1+2+|𝑚|)−(1−2+|𝑚|)

=1+|m|+1+√2+|m|−1+√2+|m|=1+|𝑚|+1+2+|𝑚|−1+2+|𝑚|

=|m|+2+2√2+|m|=|𝑚|+2+22+|𝑚|

Để điều kiện này thỏa mãn 88:

|m|+2+2√2+|m|=8|𝑚|+2+22+|𝑚|=8

|m|+2√2+|m|=6|𝑚|+22+|𝑚|=6

2√2+|m|=6−|m|22+|𝑚|=6−|𝑚|

√2+|m|=6−|m|22+|𝑚|=6−|𝑚|2

2+|m|=(6−|m|2)22+|𝑚|=(6−|𝑚|2)2

2+|m|=(6−|m|)242+|𝑚|=(6−|𝑚|)24

8+4|m|=(6−|m|)28+4|𝑚|=(6−|𝑚|)2

8+4|m|=36−12|m|+|m|28+4|𝑚|=36−12|𝑚|+|𝑚|2

|m|2−16|m|+28=0|𝑚|2−16|𝑚|+28=0

Giải phương trình bậc hai:

|m|=16±√162−4⋅282|𝑚|=16±162−4⋅282

|m|=16±√256−1122|𝑚|=16±256−1122

|m|=16±√1442|𝑚|=16±1442

|m|=16±122|𝑚|=16±122

|m|=14 hoặc 2|𝑚|=14 hoặc 2

Vậy các giá trị của m𝑚 để thỏa mãn điều kiện là m=±14𝑚=±14 hoặc m=±2𝑚=±2.

### Sự Cần Thiết của Việc Nỗ Lực Phát Huy Tiềm Năng của Bản Thân

Mỗi người sinh ra đều có những khả năng và tiềm năng riêng biệt. Việc nhận thức và nỗ lực phát huy những tiềm năng đó không chỉ giúp chúng ta đạt được thành công trong cuộc sống mà còn mang lại ý nghĩa và sự thỏa mãn cá nhân. Đây là một yếu tố quan trọng, không thể thiếu đối với sự phát triển toàn diện của mỗi con người.

#### Đạt được Mục tiêu và Thành công

Một trong những lý do chính khiến chúng ta cần nỗ lực phát huy tiềm năng bản thân là để đạt được mục tiêu và thành công. Mỗi người đều có những ước mơ và mục tiêu riêng, nhưng không phải ai cũng có thể hiện thực hóa chúng. Việc nhận biết và phát huy tiềm năng cá nhân giúp chúng ta xác định rõ ràng mục tiêu trong cuộc sống và sự nghiệp. Khi hiểu rõ khả năng và giới hạn của bản thân, chúng ta có thể đặt ra những mục tiêu hợp lý và khả thi, đồng thời xây dựng kế hoạch cụ thể để đạt được chúng.

Đạt được thành công không phải là điều dễ dàng. Nó đòi hỏi sự kiên trì, nỗ lực không ngừng nghỉ và tinh thần không bỏ cuộc. Những người không ngừng cố gắng và phát huy tiềm năng của mình thường là những người đạt được những thành tựu đáng kể, vượt qua khó khăn và thử thách để vươn lên trong cuộc sống. Nỗ lực này không chỉ mang lại thành công cá nhân mà còn góp phần vào sự phát triển chung của xã hội.

#### Phát triển Kỹ năng và Kiến thức

Học hỏi và phát triển không ngừng là một phần không thể thiếu của việc phát huy tiềm năng bản thân. Trong một thế giới luôn thay đổi và phát triển, việc không ngừng nâng cao kỹ năng và kiến thức giúp chúng ta bắt kịp xu hướng, nâng cao năng lực cạnh tranh và sẵn sàng đối mặt với những thách thức mới. Việc nỗ lực học hỏi và rèn luyện không chỉ giúp chúng ta giỏi hơn trong lĩnh vực chuyên môn mà còn mở ra những cơ hội mới trong cuộc sống và sự nghiệp.

#### Xây dựng Tự tin và Độc lập

Khi chúng ta nỗ lực phát huy tiềm năng của mình, chúng ta sẽ cảm thấy tự tin hơn về bản thân. Tự tin là yếu tố quan trọng giúp chúng ta dám nghĩ, dám làm và dám đương đầu với những khó khăn. Sự tự tin này không chỉ giúp chúng ta đạt được mục tiêu mà còn giúp chúng ta trở nên độc lập và tự chủ hơn trong cuộc sống. Khi tự tin vào khả năng của mình, chúng ta sẽ không dễ dàng bị khuất phục trước những thất bại và luôn tìm cách vươn lên, cải thiện và phát triển bản thân.

#### Tìm Kiếm Ý Nghĩa và Sự Hài Lòng

Cuộc sống sẽ trở nên có ý nghĩa hơn khi chúng ta không ngừng nỗ lực để phát huy những tiềm năng của mình. Sự hài lòng không chỉ đến từ những thành tựu mà chúng ta đạt được, mà còn từ quá trình nỗ lực và phấn đấu không ngừng. Mỗi bước tiến bộ, mỗi thành quả nhỏ trong hành trình phát triển bản thân đều mang lại niềm vui và sự thỏa mãn. Đây chính là động lực để chúng ta tiếp tục cố gắng, khám phá và khai thác tối đa tiềm năng của mình.

#### Góp Phần vào Sự Phát Triển của Xã hội

Khi mỗi cá nhân phát huy được tiềm năng của mình, họ không chỉ mang lại lợi ích cho bản thân mà còn đóng góp vào sự phát triển chung của xã hội. Những cá nhân xuất sắc trong các lĩnh vực khác nhau sẽ tạo ra những đổi mới, cải tiến và giải pháp cho các vấn đề xã hội. Sự phát triển của mỗi cá nhân góp phần xây dựng một xã hội tiến bộ, văn minh và thịnh vượng hơn.

### Kết luận

Nỗ lực phát huy tiềm năng của bản thân là một hành trình dài và đầy thử thách, nhưng đó là một hành trình đáng giá. Nó không chỉ mang lại thành công và sự thỏa mãn cá nhân mà còn đóng góp vào sự phát triển chung của xã hội. Vì vậy, mỗi chúng ta cần nhận thức được tầm quan trọng của việc phát huy tiềm năng bản thân, không ngừng nỗ lực học hỏi, rèn luyện và phát triển để trở thành phiên bản tốt nhất của chính mình.
 

Để xác định kiểu nhà nước có bản chất khác, chúng ta có thể xem xét các kiểu nhà nước phổ biến sau:

1. **Nhà nước quân chủ (Monarchy)**: Đây là kiểu nhà nước trong đó quyền lực tối cao nằm trong tay một người đứng đầu, thường là vua hoặc hoàng hậu. Quyền lực này thường được truyền từ thế hệ này sang thế hệ khác trong một dòng họ.

2. **Nhà nước cộng hòa (Republic)**: Đây là kiểu nhà nước mà quyền lực tối cao thuộc về nhân dân, được thực hiện thông qua các đại diện được bầu cử. Người đứng đầu nhà nước thường là tổng thống.

3. **Nhà nước liên bang (Federal State)**: Đây là kiểu nhà nước bao gồm nhiều đơn vị chính trị hoặc hành chính (như bang, tỉnh) có một mức độ tự trị nhất định, nhưng đều phải tuân thủ theo chính quyền trung ương.

4. **Nhà nước độc tài (Dictatorship)**: Đây là kiểu nhà nước mà quyền lực tập trung vào tay một người hoặc một nhóm nhỏ người, thường không được kiểm soát bởi các quy tắc dân chủ.

5. **Nhà nước dân chủ (Democracy)**: Đây là kiểu nhà nước mà quyền lực tối cao nằm trong tay nhân dân, thông qua các cuộc bầu cử tự do và công bằng.

Trong số các kiểu nhà nước này, kiểu nhà nước độc tài (Dictatorship) có bản chất khác biệt so với các kiểu nhà nước còn lại, vì nó tập trung quyền lực vào một cá nhân hoặc một nhóm nhỏ, thường không dựa trên các nguyên tắc dân chủ hay quyền lực nhân dân. Các kiểu nhà nước khác (quân chủ, cộng hòa, liên bang, dân chủ) đều có một mức độ phân quyền và cơ chế giám sát quyền lực nhất định, dù cách thức tổ chức và vận hành có thể khác nhau.
 

“Ôi đảo Sinh Tồn, hòn đảo thân yêu

Dẫu chẳng có mưa, chúng tôi vẫn sinh tồn trên mặt đảo

Đảo vẫn sinh tồn trên đại dương đầy gió bão

Chúng tôi như hòn đá ngàn năm, đập trong trái tim người

Như đá vững bền, như đá tốt tươi…”

Những câu thơ trên của Trần Đăng Khoa đã cho thấy sức sống mãnh liệt và tình yêu quê hương đất nước của những người lính sống trên đảo Sinh TỒn. Qua đó tác giả nhắc nhở thế hệ trẻ chúng ta hôm nay: Bất cứ thời đại nào, mỗi con người chúng ta nhất là thế hệ thanh niên cũng luôn phải ý thức vai trò trách nhiệm của mình đối với đất nước. Trước tiên thế hệ trẻ phải xác định tư tưởng, tình cảm, lí tưởng sống của mình: yêu quê hương đất nước, tự hào tự tôn dân tộc, có ý thức bảo vệ chủ quyền lãnh thổ của dân tộc; lao động, học tập để khẳng định bản lĩnh, tài năng cá nhân và phục vụ cống hiến cho đất nước, sẵn sàng có mặt khi Tổ Quốc cần. Thời đại ngày nay, xu thế toàn cầu là xu thế hội nhập, khoa học kĩ thuật phát triển với tốc độ cao, vậy thế hệ trẻ cần phải học tập tích lũy tri thức để góp phần phát triển đất nước theo kịp thời đại, hội nhập với xu thế phát triển chung của quốc tế. Bên cạnh đó, phải rèn luyện sức khỏe để có khả năng cống hiến và bảo vệ đất nước. Đồng thời thanh niên cũng cần quan tâm theo dõi đến tình hình chung của đất nước, tỉnh táo trước hành động của mình không bị kẻ xấu lợi dụng. Về vấn đề chủ quyền biển đảo, thanh niên cần hưởng ứng và tích cực các diễn đàn hợp pháp trên các phương tiện thông tin đại chúng, trên Internet, khẳng định chủ quyền biển đảo của Việt Nam trên các diễn đàn, đồng thời kịch liệt lên án và đấu tranh tham gia ngăn chặn các hành vi vi phạm xâm phạm chủ quyền biển, hải đảo thiêng liêng của Tổ Quốc, phải luôn có “trái tim nóng, cái đầu lạnh”.

Như vậy, xây dựng và bảo vệ tổ quốc là trách nhiệm thiêng liêng của thanh niên nói riêng và của mỗi con người Việt Nam nói chung. Chúng ta cần ra sức học tập và rèn luyện để trở thành những công dân ưu tú nhất, đem sức trẻ và tài năng của mình cống hiến cho sự nghiệp xây dựng và phát triển Tổ Quốc. Không bao giờ cho phép bản thân đầu hàng trước nghịch cảnh tai ương.
 

Để giải bài toán này, chúng ta cần xác định số hạt mang điện và không mang điện trong hai nguyên tử a𝑎 và b𝑏.

Gọi:
- Za𝑍𝑎 là số proton của nguyên tử a𝑎,
- Na𝑁𝑎 là số neutron của nguyên tử a𝑎,
- Zb𝑍𝑏 là số proton của nguyên tử b𝑏,
- Nb𝑁𝑏 là số neutron của nguyên tử b𝑏.

Ta có các thông tin sau:
1. Tổng số hạt trong hai nguyên tử a𝑎 và b𝑏 là 142:
Za+Na+Zb+Nb=142𝑍𝑎+𝑁𝑎+𝑍𝑏+𝑁𝑏=142

2. Số hạt mang điện (proton) nhiều hơn số hạt không mang điện (neutron) là 42:
Za+Zb−(Na+Nb)=42𝑍𝑎+𝑍𝑏−(𝑁𝑎+𝑁𝑏)=42

3. Số hạt mang điện của b𝑏 nhiều hơn số hạt mang điện của a𝑎 là 12:
Zb−Za=12𝑍𝑏−𝑍𝑎=12

Bây giờ, ta sẽ giải hệ phương trình này:

**Bước 1: Xử lý các phương trình để tìm ra Za𝑍𝑎 và Zb𝑍𝑏**

Từ phương trình thứ ba:
Zb=Za+12𝑍𝑏=𝑍𝑎+12

Thay vào phương trình thứ hai:
Za+(Za+12)−(Na+Nb)=42𝑍𝑎+(𝑍𝑎+12)−(𝑁𝑎+𝑁𝑏)=42
2Za+12−(Na+Nb)=422𝑍𝑎+12−(𝑁𝑎+𝑁𝑏)=42
2Za−(Na+Nb)=302𝑍𝑎−(𝑁𝑎+𝑁𝑏)=30
Na+Nb=2Za−30(i)𝑁𝑎+𝑁𝑏=2𝑍𝑎−30(𝑖)

**Bước 2: Thay Na+Nb𝑁𝑎+𝑁𝑏 từ phương trình (i) vào phương trình thứ nhất:**
Za+(2Za−30)+Zb+Nb=142𝑍𝑎+(2𝑍𝑎−30)+𝑍𝑏+𝑁𝑏=142
Za+2Za−30+Zb+Nb=142𝑍𝑎+2𝑍𝑎−30+𝑍𝑏+𝑁𝑏=142
3Za−30+Zb+Nb=1423𝑍𝑎−30+𝑍𝑏+𝑁𝑏=142

Do Zb=Za+12𝑍𝑏=𝑍𝑎+12, ta thay vào:
3Za−30+(Za+12)+Nb=1423𝑍𝑎−30+(𝑍𝑎+12)+𝑁𝑏=142
4Za−18+Nb=1424𝑍𝑎−18+𝑁𝑏=142
4Za+Nb=160(ii)4𝑍𝑎+𝑁𝑏=160(𝑖𝑖)

**Bước 3: Thay Nb𝑁𝑏 từ phương trình (ii) vào phương trình (i):**
Nb=160−4Za𝑁𝑏=160−4𝑍𝑎

Na+(160−4Za)=2Za−30𝑁𝑎+(160−4𝑍𝑎)=2𝑍𝑎−30
Na+160−4Za=2Za−30𝑁𝑎+160−4𝑍𝑎=2𝑍𝑎−30
Na+160=6Za−30𝑁𝑎+160=6𝑍𝑎−30
Na=6Za−190(iii)𝑁𝑎=6𝑍𝑎−190(𝑖𝑖𝑖)

**Bước 4: Giải hệ phương trình để tìm Za𝑍𝑎 và Zb𝑍𝑏:**
4Za+Nb=1604𝑍𝑎+𝑁𝑏=160
Na+Nb=2Za−30𝑁𝑎+𝑁𝑏=2𝑍𝑎−30

Thay Na𝑁𝑎 từ phương trình (iii) vào phương trình thứ nhất:
6Za−190+Nb=1606𝑍𝑎−190+𝑁𝑏=160
Nb=160−4Za𝑁𝑏=160−4𝑍𝑎

Kết hợp hai phương trình:
6Za−190+(160−4Za)=2Za−306𝑍𝑎−190+(160−4𝑍𝑎)=2𝑍𝑎−30
2Za−30=2Za−302𝑍𝑎−30=2𝑍𝑎−30

Điều này đúng, ta kiểm tra giá trị của Za𝑍𝑎:
Na=6Za−190𝑁𝑎=6𝑍𝑎−190
Nb=160−4Za𝑁𝑏=160−4𝑍𝑎

Đặt Nb=160−4Za𝑁𝑏=160−4𝑍𝑎 và Na=6Za−190𝑁𝑎=6𝑍𝑎−190, ta tính:
Tổng số hạt của a𝑎 và b𝑏 phải là:
Za+(6Za−190)+(Za+12)+(160−4Za)=142𝑍𝑎+(6𝑍𝑎−190)+(𝑍𝑎+12)+(160−4𝑍𝑎)=142

**Tính Za𝑍𝑎:**
2Za+6Za−4Za=322𝑍𝑎+6𝑍𝑎−4𝑍𝑎=32
4Za=324𝑍𝑎=32
Za=8𝑍𝑎=8

**Tính các giá trị còn lại:**
Zb=Za+12=20𝑍𝑏=𝑍𝑎+12=20
Na=6Za−190=48−190=−142𝑁𝑎=6𝑍𝑎−190=48−190=−142
Nb=160−4Za=160−32=128𝑁𝑏=160−4𝑍𝑎=160−32=128

Từ đó, số khối của hai nguyên tử là:
- Nguyên tử a𝑎: 8 proton, 4 neutron
- Nguyên tử b𝑏: 20 proton, 18 neutron
 

My house is next to the supermarket

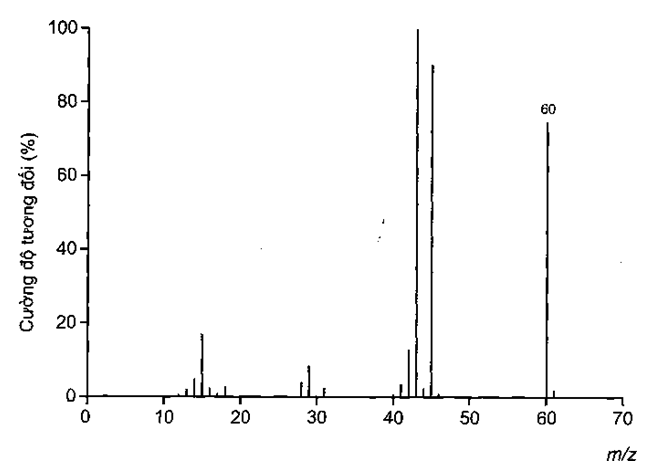
Dựa vào peak [M+] có giá trị m/z lớn nhất của (E) => M(E)= 60.

Vì (E) có 53,33% oxygen về khối lượng nên công thức phân tử của (E) là C2H4O2.

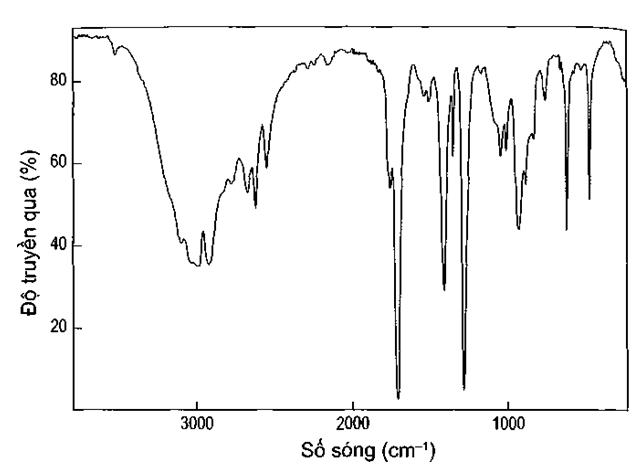
Dựa vào kết quả phổ IR có các tín hiệu cực tiểu truyền qua ứng với số sóng (cm-1): - nằm trong khoảng 1 725 - 1 700 cm-1 => có liên kết C=O.

- nằm trong khoảng 3 300 - 2 500 cm-1 => có liên kết O-H.

=> (E) có nhóm chức -COOH.

Vậy công thức cấu tạo của (E) là CH3COOH (acetic acid).

Trong quá khứ, gương rất hiếm và có giá trị, được làm từ các tấm đồng hoặc bạc đánh bóng. Mặc dù đắt tiền nhưng chúng thường chỉ tạo ra hình ảnh bị cong vênh, mờ và gương nhanh ố. Sau đó chuyển sang sử dụng thuỷ ngân tráng sau tấm kính phẳng. Tuy nhiên, việc làm này lại gây nguy hiểm vì thuỷ ngân là nguyên nhân gây ngộ độc cho người sản xuất.

Ngày nay, gương soi đã được thay thế bằng bạc tráng sau tấm kính nhờ phản ứng của aldehyde (R-CHO) hay glucose với dung dịch AgNO3 trong NH3 dư.

RCHO + 2[Ag(NH3)2]OH → RCOONH4 + 2Ag↓ + 3NH3 + H2O

C6H12O6 + 2[Ag(NH3)2]OH → C5H11O5COONH4 + 2Ag↓ + 3NH3 + H2O

Kim loại Ag kết tủa tạo ra bám chặt vào gương, người ta quét lên mặt sau chiếc gương một lớp sơn dầu bảo vệ. Do bề mặt kính và lớp bạc rất mịn nên hình ảnh được phản chiếu tốt, không bị cong vênh. Ngoài phản chiếu hình ảnh, lớp tráng bạc được dùng trong lớp vỏ của phích nước (bình thuỷ), giúp duy trì nhiệt độ trong một thời gian dài.
 

Để giải quyết các câu hỏi này, chúng ta sẽ thực hiện từng bước một.

### Câu 1:
#### a) M +(2x³ - x²y + 1) = -x³ + 3x²y + 2
Để tìm giá trị của M, chúng ta cần so sánh các hệ số của các biểu thức tương đương:
- Hệ số của x3𝑥3: 1+2=31+2=3
- Hệ số của x2y𝑥2𝑦: −1=−1−1=−1
- Hệ số của hạng tự do: 1=21=2

Vì vậy, ta có: M=3x3−x2y+1−2=3x3−x2y−1𝑀=3𝑥3−𝑥2𝑦+1−2=3𝑥3−𝑥2𝑦−1.

#### b) M - (x² - 6x + 9) = 0
Đây là một phương trình đa thức, ta cần giải phương trình này để tìm giá trị của M.
M−(x2−6x+9)=0𝑀−(𝑥2−6𝑥+9)=0
M−x2+6x−9=0𝑀−𝑥2+6𝑥−9=0
M=x2−6x+9𝑀=𝑥2−6𝑥+9

Vậy, M=x2−6x+9𝑀=𝑥2−6𝑥+9.

### Câu 2:
#### a) C = A + B
A=x2−2y2+xy+1𝐴=𝑥2−2𝑦2+𝑥𝑦+1
B=x2+y2−x2y2−1𝐵=𝑥2+𝑦2−𝑥2𝑦2−1
C=(x2−2y2+xy+1)+(x2+y2−x2y2−1)𝐶=(𝑥2−2𝑦2+𝑥𝑦+1)+(𝑥2+𝑦2−𝑥2𝑦2−1)
C=x2−2y2+xy+1+x2+y2−x2y2−1𝐶=𝑥2−2𝑦2+𝑥𝑦+1+𝑥2+𝑦2−𝑥2𝑦2−1
C=2x2−2y2+xy+y2−x2y2𝐶=2𝑥2−2𝑦2+𝑥𝑦+𝑦2−𝑥2𝑦2
C=2x2−x2y2−2y2+y2+xy𝐶=2𝑥2−𝑥2𝑦2−2𝑦2+𝑦2+𝑥𝑦
C=2x2−x2y2−y2+xy𝐶=2𝑥2−𝑥2𝑦2−𝑦2+𝑥𝑦

#### b) C + A = B
B=C+A𝐵=𝐶+𝐴
x2+y2−x2y2−1=2x2−x2y2−y2+xy+x2−2y2+xy+1𝑥2+𝑦2−𝑥2𝑦2−1=2𝑥2−𝑥2𝑦2−𝑦2+𝑥𝑦+𝑥2−2𝑦2+𝑥𝑦+1
x2+y2−x2y2−1=3x2−3y2+2xy−x2y2+1𝑥2+𝑦2−𝑥2𝑦2−1=3𝑥2−3𝑦2+2𝑥𝑦−𝑥2𝑦2+1
0=3x2−3y2+2xy−x2y20=3𝑥2−3𝑦2+2𝑥𝑦−𝑥2𝑦2
0=3x2−3y2+2xy−x2y20=3𝑥2−3𝑦2+2𝑥𝑦−𝑥2𝑦2

### Câu 3:
#### a) Tính giá trị của A:
A=x3+2xy−2x3+2x3+2x3−y3𝐴=𝑥3+2𝑥𝑦−2𝑥3+2𝑥3+2𝑥3−𝑦3
Đơn giản hóa biểu thức:
A=(x3−2x3+2x3)+2xy−y3𝐴=(𝑥3−2𝑥3+2𝑥3)+2𝑥𝑦−𝑦3
A=2xy−y3𝐴=2𝑥𝑦−𝑦3
Đặt x=2𝑥=2 và y=−3𝑦=−3:
A=2(2)(−3)−(−3)3𝐴=2(2)(−3)−(−3)3
A=−12+27𝐴=−12+27
A=15𝐴=15

#### b) Tính giá trị của B:
B=xy+x2y2−x4y4+x6y6−x8y8𝐵=𝑥𝑦+𝑥2𝑦2−𝑥4𝑦4+𝑥6𝑦6−𝑥8𝑦8
Đặt x=1𝑥=1 và y=−1𝑦=−1:
B=(1)(−1)+(1)2(−1)2−(1)4(−1)4+(1)6(−1)6−(1)8(−1)8𝐵=(1)(−1)+(1)2(−1)2−(1)4(−1)4+(1)6(−1)6−(1)8(−1)8
B=−1+1−1+1−1𝐵=−1+1−1+1−1
B=−1𝐵=−1

#### c) Tính giá trị của C:
C=xy+x2y2+x3y3+...+x10y10𝐶=𝑥𝑦+𝑥2𝑦2+𝑥3𝑦3+...+𝑥10𝑦10
Ta thấy C là tổng của các mũ của x và y từ 1 đến 10.
C=∑10n=1xnyn𝐶=∑𝑛=110𝑥𝑛𝑦𝑛

Đây chỉ là một tổng vô hạn các mũ của x và y, không thể tính toán cụ thể giá trị nếu không có giá trị cụ thể của x và y.
 

(a) 2CH3[CH2]4CHO + O2  xt,to−→→𝑥𝑡,𝑡𝑜 2CH3[CH2]4COOH

hexanal                         hexanoic acid

(b) CH3[CH2]6CHO + H2 Ni,to−−→→𝑁𝑖,𝑡𝑜 CH3[CH2]6CH2OH

octanal                          octan-1-ol

(c) CH3CH2COOH + CH3OH  H2SO4dac,t°⇌⇌𝐻2𝑆𝑂4𝑑𝑎𝑐,𝑡° CH3CH2COOCH3 + H2O

     propanoic acid                        methanol     methyl propanoate

(d) CH3CH2-CO-CH2CH2CH3 + H2   Ni,to−−→→𝑁𝑖,𝑡𝑜  CH3CH2-CH(OH)-CH2CH2CH3

        hexan-3-one                                    hexan-3-ol

(e) CH3CH2CH(CH3)CH2COOH + CH3-CH(OH)-CH3  Ni,to−−→→𝑁𝑖,𝑡𝑜

3-methylpentanoic acid         propan-2-ol

CH3CH2CH(CH3)CH2COOCH(CH3)2 + H2O

isopropyl 3-methylpentanoate

(g) CH3CH2CH(CH3)CHO + H2   Ni,to−−→→𝑁𝑖,𝑡𝑜 CH3CH2CH(CH3)CH2OH

         2-methylbutanal                            2-methylbutanol

(h) CH3CH(CH3)CH(CH3)CH2OH+O2 enzyme−−−→→enzymeCH3CH(CH3)CH(CH3)COOH + H2O

2,3-dimethylbutan-1-ol                   2,3-dimethylbutanoic acid