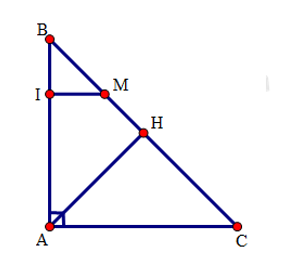
Bài 11 : Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho
CM = CA. Đường thẳng đi qua M và song song với CA cắt AB tại I.
a) Tứ giác ACMI là hình gì ?
b) Chứng minh AB + AC < AH + BC.
Quảng cáo
2 câu trả lời 2585
 a)Tứ giác ACMI có: MI //AC (gt) và ˆA=90°A^=90° (gt) nên là hình thang vuông.
a)Tứ giác ACMI có: MI //AC (gt) và ˆA=90°A^=90° (gt) nên là hình thang vuông.
b)
Xét tam giác AMCAMC có: CM=AC(gt)nên tam giác AMC cân tại C
Suy ra ˆMAC=ˆAMC(1)
Xét tam giác AMH có: ˆMAH=90∘ˆ−AMH (hai góc phụ nhau) (2)
Xét tam giác ABC vuông tại A: ˆMAB=ˆBAC−ˆMAC=90∘−ˆMAC (phụ nhau) (3)
Từ (1),(2) và (3) suy ra: ˆMAH=ˆMAB⇒ˆMAH=ˆMAI
Xét hai tam giác vuông ΔAHMvà ΔAIM có:
AM (cạnh chung)
ˆMAH=ˆMAI (cmt)
⇒ΔAHM=ΔAIM (cạnh huyền-góc nhọn)
⇒AH=AI (hai cạnh tương ứng)
Lại có: MI∥AC(gt),AC⊥AB(gt)⇒MI⊥AB
Do đó BI<BM(4) (quan hệ giữa đường vuông góc và đường xiên)
Mặt khác:
AC=CM(gt)(5
AI=AH(cmt)(6)
Cộng (6),(4),(5) vế theo vế ta được:
AI+BI+AC<AH+BM+CM
⇒AB+AC<AH+BC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
46111
Đã trả lời bởi chuyên gia
46111 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
33002
Đã trả lời bởi chuyên gia
33002 -
 Đã trả lời bởi chuyên gia
32833
Đã trả lời bởi chuyên gia
32833 -
 Đã trả lời bởi chuyên gia
28732
Đã trả lời bởi chuyên gia
28732 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
26242
Đã trả lời bởi chuyên gia
26242 -
 Đã trả lời bởi chuyên gia
25770
Đã trả lời bởi chuyên gia
25770 -
 Đã trả lời bởi chuyên gia
22938
Đã trả lời bởi chuyên gia
22938 -
 Đã trả lời bởi chuyên gia
22842
Đã trả lời bởi chuyên gia
22842



