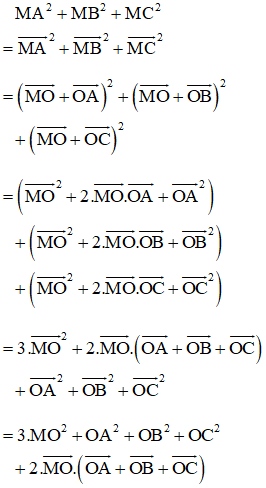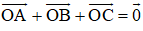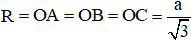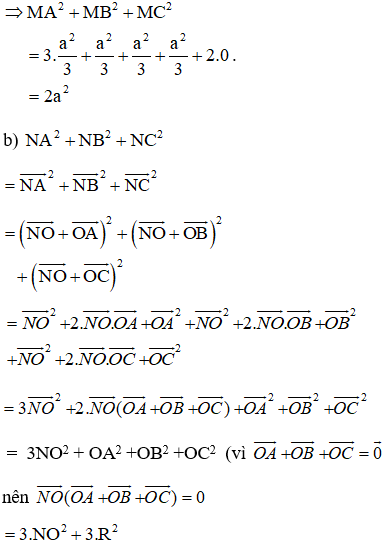Cho tam giác đều ABC cạnh a.
a, Cho M là một điểm trên đường tròn ngoại tiếp tam giác ABC. Tính MA2 + MB2 + MC2 theo a.
b, Cho đường thẳng d tùy ý, tìm điểm N trên đường thẳng d sao cho NA2 + NB2 + NC2 nhỏ nhất.
Quảng cáo
1 câu trả lời 482
a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
Lại có:
+ O là trọng tâm tam giác nên
+ Bán kính đường tròn ngoại tiếp tam giác:
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
38650
Đã trả lời bởi chuyên gia
38650 -
 Đã trả lời bởi chuyên gia
32752
Đã trả lời bởi chuyên gia
32752 -
 Đã trả lời bởi chuyên gia
28346
Đã trả lời bởi chuyên gia
28346 -
 Đã trả lời bởi chuyên gia
24784
Đã trả lời bởi chuyên gia
24784 -
 Đã trả lời bởi chuyên gia
12903
Đã trả lời bởi chuyên gia
12903
Gửi báo cáo thành công!