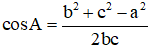Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Quảng cáo
1 câu trả lời 411
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
50889
Đã trả lời bởi chuyên gia
50889 -
 Đã trả lời bởi chuyên gia
16876
Đã trả lời bởi chuyên gia
16876 -
 Đã trả lời bởi chuyên gia
15562
Đã trả lời bởi chuyên gia
15562 -
 Đã trả lời bởi chuyên gia
13563
Đã trả lời bởi chuyên gia
13563 -
 Đã trả lời bởi chuyên gia
12648
Đã trả lời bởi chuyên gia
12648 -
 Đã trả lời bởi chuyên gia
11692
Đã trả lời bởi chuyên gia
11692 -
 Đã trả lời bởi chuyên gia
10865
Đã trả lời bởi chuyên gia
10865 -
 Đã trả lời bởi chuyên gia
9681
Đã trả lời bởi chuyên gia
9681 -
 Đã trả lời bởi chuyên gia
9656
Đã trả lời bởi chuyên gia
9656
Gửi báo cáo thành công!