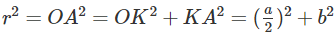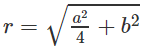Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau: BAC = 120 và b = c
Quảng cáo
1 câu trả lời 468
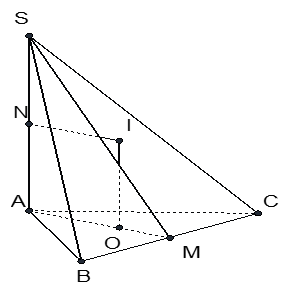
BAC = 120 và b = c, khi đó ABC là một tam giác cân có góc A ở đỉnh bằng 120 và cạnh bên bằng b. Gọi M là trung điểm của cạnh BC. Kéo dài AM một đoạn MK = AM, ta có KA = KB = KC = AB = AC = b.
Dựng đường thẳng d vuông góc với mặt phẳng (ABC) tại K. Mặt phẳng trung trực của đoạn SA cắt d tại O.
Ta có: OS = OA = OB = OC và
Do đó ta có mặt cầu tâm O ngoại tiếp tứ diện và có bán kính
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11160
Đã trả lời bởi chuyên gia
11160 -
 Đã trả lời bởi chuyên gia
8740
Đã trả lời bởi chuyên gia
8740 -
 Đã trả lời bởi chuyên gia
4268
Đã trả lời bởi chuyên gia
4268 -
 Đã trả lời bởi chuyên gia
3750
Đã trả lời bởi chuyên gia
3750
Gửi báo cáo thành công!