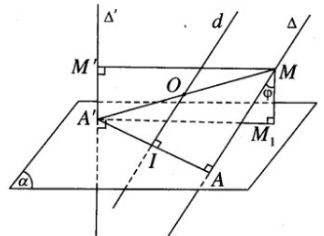
Cho hai đường thẳng chéo nhau và ′ có AA’ là đoạn vuông góc chung, trong đó A và A′ ′. Gọi () là mặt phẳng chứa AA’ và vuông góc với ′ và cho biết AA’ = a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng () lần lượt cắt và ′ tại M và M’ . Hình chiếu vuông góc của M trên mặt phẳng () là . Chứng minh rằng khi x thay đổi mặt cầu tâm O luôn luôn chứa một đường tròn cố định.
Quảng cáo
1 câu trả lời 432
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11164
Đã trả lời bởi chuyên gia
11164 -
 Đã trả lời bởi chuyên gia
8746
Đã trả lời bởi chuyên gia
8746 -
 Đã trả lời bởi chuyên gia
4270
Đã trả lời bởi chuyên gia
4270 -
 Đã trả lời bởi chuyên gia
3756
Đã trả lời bởi chuyên gia
3756