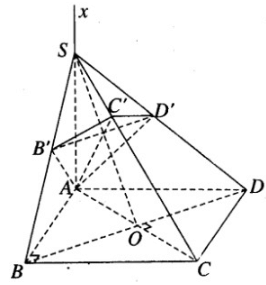
Trong mặt phẳng () cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với () ta lấy một điểm S tùy ý, dựng mặt phẳng () đi qua A và vuông góc với đường thẳng SC. Mặt phẳng () cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Quảng cáo
1 câu trả lời 293
Ta có
Ta lại có AB′ SC nên suy ra AB′ (SBC). Do đó AB′ B′C
Chứng minh tương tự ta có AD′ D′C.
Vậy ABC = AB′C = AC′C = AD′C = ADC = 90
Từ đó suy ra 7 điểm A, B, C, D, B’, C’, D’ cùng nằm trên mặt cầu đường kính là AC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11164
Đã trả lời bởi chuyên gia
11164 -
 Đã trả lời bởi chuyên gia
8746
Đã trả lời bởi chuyên gia
8746 -
 Đã trả lời bởi chuyên gia
4270
Đã trả lời bởi chuyên gia
4270 -
 Đã trả lời bởi chuyên gia
3756
Đã trả lời bởi chuyên gia
3756
Gửi báo cáo thành công!