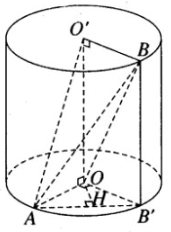
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r. Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Chứng minh rằng các mặt bên của tứ diện OABO’ là những tam giác vuông. Tính thể tích của tứ diện này.
Quảng cáo
1 câu trả lời 450
Vì trục OO’ vuông góc với các đáy nên OO′ OA; OO′ O′B. Vậy các tam giác AOO’ và BO’O vuông tại O và O’.
Theo giả thiết ta có AO O′B mà AO OO′ ⇒ AO (OO′B). Do đó, AO OB nên tam giác AOB vuông tại O. Tương tự, ta chứng minh được tam giác AO’B vuông tại O’. Thể tích hình chóp OABO’ là:
Hay
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11164
Đã trả lời bởi chuyên gia
11164 -
 Đã trả lời bởi chuyên gia
8746
Đã trả lời bởi chuyên gia
8746 -
 Đã trả lời bởi chuyên gia
4270
Đã trả lời bởi chuyên gia
4270 -
 Đã trả lời bởi chuyên gia
3756
Đã trả lời bởi chuyên gia
3756