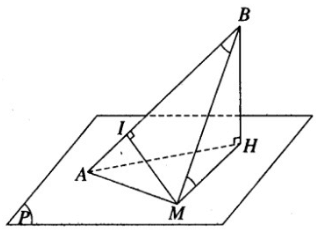
Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A. Một điểm M chạy trên mặt phẳng (P) sao cho góc ABM = BMH. Chứng minh rằng điểm M luôn luôn nằm trên một mặt trụ xoay có trục là AB.
Quảng cáo
1 câu trả lời 474
Giải sử ta có điểm M thuộc mặt phẳng (P) thỏa mãn các điều kiện của giả thiết đã cho. Gọi I là hình chiếu vuông góc của M trên AB. Hai tam giác vuông BIM và MHB bằng nhau vì có cạnh huyền chung và một cặp góc nhọn bằng nhau. Do đó MI = BH không đổi. Vậy điểm M luôn luôn nằm trên mặt trụ trục AB và có bán kính bằng BH.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11164
Đã trả lời bởi chuyên gia
11164 -
 Đã trả lời bởi chuyên gia
8746
Đã trả lời bởi chuyên gia
8746 -
 Đã trả lời bởi chuyên gia
4270
Đã trả lời bởi chuyên gia
4270 -
 Đã trả lời bởi chuyên gia
3756
Đã trả lời bởi chuyên gia
3756
Gửi báo cáo thành công!