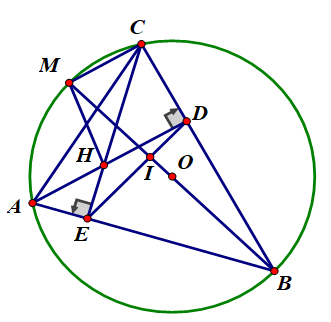
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Hai đường cao AD và CE cắt nhau tại H. Tia BO cắt (O) tại điểm thứ hai M. I là giao điểm của BM và DE
c) Chứng minh tứ giác CMID là tứ giác nội tiếp
Quảng cáo
1 câu trả lời 492
5 năm trước
c) Do tứ giác AEDC là tứ giác nội tiếp nên ∠(CAB) = ∠(IDB) (cùng bù ∠(CDE) )
Mặt khác ∠(CAB) = ∠(CMB) (2 góc nội tiếp cùng chắn cung BC)
⇒ ∠(CMB) = ∠(IDB)
⇒ Tứ giác CMID là tứ giác nội tiếp ( Góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17108
Đã trả lời bởi chuyên gia
17108 -
 Đã trả lời bởi chuyên gia
15553
Đã trả lời bởi chuyên gia
15553 -
 Đã trả lời bởi chuyên gia
15092
Đã trả lời bởi chuyên gia
15092 -
11422
-
11256
-
 Đã trả lời bởi chuyên gia
9503
Đã trả lời bởi chuyên gia
9503 -
 Đã trả lời bởi chuyên gia
7165
Đã trả lời bởi chuyên gia
7165
Gửi báo cáo thành công!