Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2, AB = a; BC = 2a. Gọi M là trung điểm của DC. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng
A.
B.
C.
D.
Quảng cáo
1 câu trả lời 1175
Phương pháp:
Xác định chiều cao hình chóp bằng kiến thức 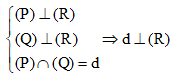
Xác định khoảng cách ![]()
Tính toán bằng cách sử dụng quan hệ diện tích, định lý hàm số cosin, công thức tính diện tích tam giác S = a.h với a là cạnh đáy, h là chiều cao tương ứng và ![]()
Cách giải:
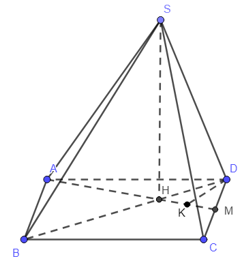
Gọi H = AMBD
Ta có 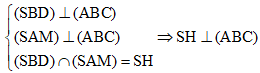
Vì AB//CD nên theo định lý Ta-lét ta có

Ta có ![]()
![]()
![]()
Vì M là trung điểm của DC và ABCD là hình bình hành có diện tích 2 nên ta có:
![]()
Lại có CD = AB = a ![]()
Khi đó ![]()
![]()
![]()
![]()
![]()
![]()
Lại có ![]()
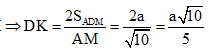
Từ đó ![]()
Chọn: C
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11145
Đã trả lời bởi chuyên gia
11145 -
 Đã trả lời bởi chuyên gia
10200
Đã trả lời bởi chuyên gia
10200