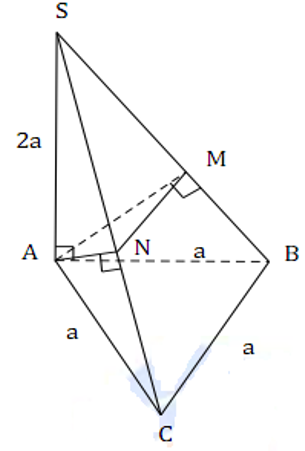
Xét tứ diện ABCD có các cạnh AC=CD=DB=BA=2 và AD, BC thay đổi. Giá trị lớn nhất của thể tích tứ diện ABCD bằng:
A.
B.
C.
D.
Quảng cáo
1 câu trả lời 2210
5 năm trước
Chọn B
Gọi M, N lần lượt là trung điểm AD và BC.
Theo giả thiết ta có: ABD và ACD là các tam giác cân có M là trung điểm của AD nên:
Trong tam giác ΔMBC có MN vừa là đường cao vừa là trung tuyến nên
Khi đó diện tích tam giác ΔMBC là:
Thể tích tứ diện ABCD là:
Đặt AD=x, BC=y ta có:
Dấu bằng xảy ra khi x=y.
Ta lại có:
Dấu bằng xảy ra khi:
Vậy giá trị lớn nhất của thể tích khối tứ diện ABCD là:
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
Gửi báo cáo thành công!