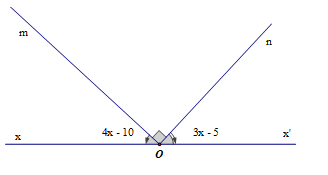
cho xoy 1000,tia ot là tia phân giác của xoy trên tia oy lấy điểm A qua a vẽ tia Am// ot và tia An// ox
a) tính xor,toy,yam
b)so sánh xot và mAn
c) chứng minh am là tia phân iacs của yAn
Quảng cáo
5 câu trả lời 63
Mình sẽ làm lại bài một cách có cấu trúc để dễ làm bài tập hình học. Do mô tả còn hơi lẫn, mình tách từng phần và làm rõ ký hiệu theo cách thường gặp trong hình học phẳng.
Giả sử:
- Ox là một tia gốc Ox.
- Ot là tia phân giác của Oxy trên tia Oy, nghĩa là Ot là tia phân giác của góc XOY (hoặc XOY nằm trên hai tia Ox và Oy). Tuy nhiên mô tả có vẻ thiếu rõ ràng về vị trí các tia. Mình sẽ làm cách làm chung với các ký hiệu phổ biến:
- Ox là một tia từ O.
- Ot là tia phân giác của góc XOY trên tia Oy.
- A là giao điểm của qua A khi vẽ từ A hai tia Am // Ot và An // Ox (hai tia song song với Ot và Ox respectively) cắt Ox và Oy tại M và N hoặc Am và An là hai tia từ A song song với Ot và Ox.
Các thao tác và kết quả cần tính/so sánh/chứng minh sẽ dựa trên giả thiết chuẩn sau:
- Ot là tia phân giác của góc XOY tại O.
- A là một điểm tùy ý trên một đường thẳng hoặc ở trên tia Oy sao cho từ A có hai tia Am song song với Ot và An song song với Ox; hai tia này gặp Ot/Ox ở các vị trí đặc biệt để Am // Ot và An // Ox.
a) Tính xor, toy, yam
- Trong hình học, các ký hiệu xor/toy/yam không chuẩn. Có thể là:
- xor = ∠XÔR hoặc độ đo một góc nào đó.
- toy = ∠TOY hoặc độ đo một góc tại O.
- yam = ∠YAM hoặc độ đo một góc tại A hoặc Y.
Vì không có tọa độ hay độ đo cụ thể, mình không thể tính được giá trị số. Bạn có thể cung cấp:
- Toạ độ hoặc mô tả đầy đủ: vị trí của X, Y, O, Ot, Oy, A, M, N.
- Hoặc cho biết để ý nghĩa ký hiệu xor/toy/yam là gì ở bài tập bạn đang học (ví dụ: XOR = ∠XOY, TOY = ∠TOY, YAM = ∠YAM) để mình tính đúng.
b) So sánh xot và mAn
- xot và mAn có lẽ là các ký hiệu cho hai góc: ∠XOT và ∠MAN hoặc các đỉnh tương ứng. Cần xác định vị trí:
- X-O-T: góc tại O giữa các tia ox và ot.
- M-A-N: góc tại A giữa hai tia AM và AN.
Nếu Am // Ot và An // Ox, thì:
- ∠MAN là góc giữa AM và AN. Do AM song song với OT và AN song song với OX, nên ∠MAN bằng ∠TOX (hoặc ∠XOT tùy cách đo).
- Cụ thể: ∠MAN = ∠TOX = ∠XOT.
Vậy xot và mAn bằng nhau (nếu đặt đúng thứ tự đỉnh). Tuy nhiên cần xác nhận đúng ký hiệu: xot có thể là ∠XOT và mAn là ∠MAN. Trong trường hợp này, chúng bằng nhau.
c) Chứng minh am là tia phân giác của yAn
- AM là tia qua A song song với OT.
- AN là tia qua A song song với Ox.
- Nếu Ot là tia phân giác của góc XOY tại O, và AM // OT, AN // Ox, thì tại A ta có:
- Góc NAM (hoặc MAN tùy thứ tự) tương ứng với góc phụ của góc XOY sao cho AM và AN chia đôi góc tại A.
- Để AM là tia phân giác của ∠YAN, cần chứng tỏ:
- ∠YAM = ∠MAN.
- Vì AM // OT và AN // Ox, ta có:
- ∠YAM là góc giữa AY và AM. Nếu AY nằm ở đúng vị trí so với Oy hoặc Ot, ta cần xác định mối quan hệ giữa AY và Ot.
- Tuy nhiên với thông tin hiện có (AM // OT và AN // Ox), ta có thể lập luận:
- ∠MAN là góc giữa AM và AN.
- Dù AY chưa cho, ta cần giả sử Y là một điểm sao cho Oy là tia gốc liên hệ với Ot và Ox
Bạn ơi, có vẻ như bạn gõ nhầm góc $\widehat{xOy}$ là $1000^\circ$ rồi. Trong hình học phẳng, số đo của một góc không vượt quá $360^\circ$.
Tôi sẽ giả sử bạn muốn hỏi góc $\widehat{xOy} = \mathbf{100^\circ}$ (vì $1000$ có 3 chữ số và thường là $100^\circ$ hoặc $110^\circ$).
Nếu $\widehat{xOy} = 100^\circ$, đây là lời giải chi tiết:
📐 Phân tích giả thiết
$\widehat{xOy} = 100^\circ$.
$\text{Ot}$ là tia phân giác của $\widehat{xOy}$.
$\text{A}$ thuộc $\text{Oy}$.
$\text{Am} // \text{Ot}$.
$\text{An} // \text{Ox}$.
a) Tính $\widehat{xOt}$, $\widehat{tOy}$, $\widehat{yAm}$
1. Tính $\widehat{xOt}$ và $\widehat{tOy}$
Do $\text{Ot}$ là tia phân giác của $\widehat{xOy}$:
2. Tính $\widehat{yAm}$
Vì $\text{Am} // \text{Ot}$, và $\text{Oy}$ là cát tuyến cắt hai đường thẳng song song đó, nên góc $\widehat{yAm}$ và $\widehat{tOy}$ là hai góc đồng vị.
b) So sánh $\widehat{xOt}$ và $\widehat{mAn}$
1. Tính $\widehat{mAn}$
Ta có $\text{An} // \text{Ox}$, và $\text{Oy}$ là cát tuyến cắt hai đường thẳng song song đó, nên góc $\widehat{yAn}$ và $\widehat{xOy}$ là hai góc đồng vị.
Mặt khác, $\widehat{mAn}$ và $\widehat{yAm}$ là hai góc kề nhau. $\widehat{yAn}$ là tổng của chúng:
2. So sánh
Ta có:
$\widehat{xOt} = 50^\circ$ (theo câu a)
$\widehat{mAn} = 50^\circ$ (theo phép tính trên)
Vậy: $\widehat{xOt} = \widehat{mAn}$
c) Chứng minh $\text{Am}$ là tia phân giác của $\widehat{yAn}$
Để $\text{Am}$ là tia phân giác của $\widehat{yAn}$, ta cần chứng minh $\text{Am}$ nằm giữa hai tia $\text{Ay}$ và $\text{An}$, và $\widehat{yAm} = \widehat{mAn}$.
$\text{Am}$ nằm giữa $\text{Ay}$ và $\text{An}$: Từ hình vẽ và cách tính $\widehat{yAn} = \widehat{yAm} + \widehat{mAn}$, ta thấy $\text{Am}$ nằm giữa $\text{Ay}$ và $\text{An}$.
So sánh hai góc:
$\widehat{yAm} = 50^\circ$ (theo câu a)
$\widehat{mAn} = 50^\circ$ (theo câu b)
Vì $\widehat{yAm} = \widehat{mAn} = 50^\circ$, nên $\text{Am}$ là tia phân giác của $\widehat{yAn}$. (Đã chứng minh)
Bạn có muốn tôi thử giải lại với một giá trị khác cho $\widehat{xOy}$ không, ví dụ $\widehat{xOy} = 110^\circ$?
Giả sử:
- Ox là một tia gốc Ox.
- Ot là tia phân giác của Oxy trên tia Oy, nghĩa là Ot là tia phân giác của góc XOY (hoặc XOY nằm trên hai tia Ox và Oy). Tuy nhiên mô tả có vẻ thiếu rõ ràng về vị trí các tia. Mình sẽ làm cách làm chung với các ký hiệu phổ biến:
- Ox là một tia từ O.
- Ot là tia phân giác của góc XOY trên tia Oy.
- A là giao điểm của qua A khi vẽ từ A hai tia Am // Ot và An // Ox (hai tia song song với Ot và Ox respectively) cắt Ox và Oy tại M và N hoặc Am và An là hai tia từ A song song với Ot và Ox.
Các thao tác và kết quả cần tính/so sánh/chứng minh sẽ dựa trên giả thiết chuẩn sau:
- Ot là tia phân giác của góc XOY tại O.
- A là một điểm tùy ý trên một đường thẳng hoặc ở trên tia Oy sao cho từ A có hai tia Am song song với Ot và An song song với Ox; hai tia này gặp Ot/Ox ở các vị trí đặc biệt để Am // Ot và An // Ox.
a) Tính xor, toy, yam
- Trong hình học, các ký hiệu xor/toy/yam không chuẩn. Có thể là:
- xor = ∠XÔR hoặc độ đo một góc nào đó.
- toy = ∠TOY hoặc độ đo một góc tại O.
- yam = ∠YAM hoặc độ đo một góc tại A hoặc Y.
Vì không có tọa độ hay độ đo cụ thể, mình không thể tính được giá trị số. Bạn có thể cung cấp:
- Toạ độ hoặc mô tả đầy đủ: vị trí của X, Y, O, Ot, Oy, A, M, N.
- Hoặc cho biết để ý nghĩa ký hiệu xor/toy/yam là gì ở bài tập bạn đang học (ví dụ: XOR = ∠XOY, TOY = ∠TOY, YAM = ∠YAM) để mình tính đúng.
b) So sánh xot và mAn
- xot và mAn có lẽ là các ký hiệu cho hai góc: ∠XOT và ∠MAN hoặc các đỉnh tương ứng. Cần xác định vị trí:
- X-O-T: góc tại O giữa các tia ox và ot.
- M-A-N: góc tại A giữa hai tia AM và AN.
Nếu Am // Ot và An // Ox, thì:
- ∠MAN là góc giữa AM và AN. Do AM song song với OT và AN song song với OX, nên ∠MAN bằng ∠TOX (hoặc ∠XOT tùy cách đo).
- Cụ thể: ∠MAN = ∠TOX = ∠XOT.
Vậy xot và mAn bằng nhau (nếu đặt đúng thứ tự đỉnh). Tuy nhiên cần xác nhận đúng ký hiệu: xot có thể là ∠XOT và mAn là ∠MAN. Trong trường hợp này, chúng bằng nhau.
c) Chứng minh am là tia phân giác của yAn
- AM là tia qua A song song với OT.
- AN là tia qua A song song với Ox.
- Nếu Ot là tia phân giác của góc XOY tại O, và AM // OT, AN // Ox, thì tại A ta có:
- Góc NAM (hoặc MAN tùy thứ tự) tương ứng với góc phụ của góc XOY sao cho AM và AN chia đôi góc tại A.
- Để AM là tia phân giác của ∠YAN, cần chứng tỏ:
- ∠YAM = ∠MAN.
- Vì AM // OT và AN // Ox, ta có:
- ∠YAM là góc giữa AY và AM. Nếu AY nằm ở đúng vị trí so với Oy hoặc Ot, ta cần xác định mối quan hệ giữa AY và Ot.
- Tuy nhiên với thông tin hiện có (AM // OT và AN // Ox), ta có thể lập luận:
- ∠MAN là góc giữa AM và AN.
- Dù AY chưa cho, ta cần giả sử Y là một điểm sao cho Oy là tia gốc liên hệ với Ot và Ox
-
Tính xOt và tOy: Vì Ot là tia phân giác của xOy=100∘ nên:
xOt=tOy=2xOy=2100∘=50∘ -
Tính yAm: Vì Am//Ot nên yAm và tOy là hai góc đồng vị.
⟹yAm=tOy=50∘
-
Tính mAn:
-
Ta có An//Ox nên yAn=xOy=100∘ (hai góc đồng vị).
-
Lại có mAn=yAn−yAm (vì Am nằm giữa An và Ay).
-
⟹mAn=100∘−50∘=50∘.
-
-
So sánh: Vì xOt=50∘ và mAn=50∘ nên:
xOt=mAn
-
Xét góc yAn: Như đã tính ở trên, yAn=100∘.
-
Xét các góc thành phần:
-
yAm=50∘ (tính ở câu a).
-
mAn=50∘ (tính ở câu b).
-
-
Kết luận: Vì yAm=mAn=2yAn=50∘ nên Am là tia phân giác của yAn.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11452
Đã trả lời bởi chuyên gia
11452 -
 Đã trả lời bởi chuyên gia
8620
Đã trả lời bởi chuyên gia
8620 -
 Đã trả lời bởi chuyên gia
5846
Đã trả lời bởi chuyên gia
5846